-
AutoCor: Análisis de autocorrelación espacial (Moran)
AutoCor: Análisis de autocorrelación espacial (Moran)| Presentación | Caja de diálogo de la aplicación |
| Sintaxis |
Esta aplicación permite cuantificar el grado de autocorrelación espacial de una variable en un fichero ráster mediante el cálculo de un indicador, en este caso el índice I(i) de Moran.
La autocorrelación espacial es una propiedad presente en la distribución espacial de una variable si los valores en cualquier localización están influenciados por valores de localizaciones cercanas (siguiendo la primera ley de la Geografía de Tobler https://en.wikipedia.org/wiki/Tobler%27s_first_law_of_geography). El concepto "cercano" quedará referido al umbral de autocorrelación, distancia límite donde la autocorrelación es muy baja o inexistente. Este umbral resulta útil para imponer las condiciones espaciales idóneas sobre el muestreo de la variable y determinados modelos estadísticos asociados.
El índice I de Moran se calcula con la siguiente fórmula:
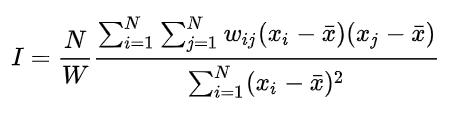
donde:
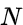es el número de unidades espaciales, indexadas por i y j; 
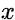es la variable de interés; 
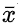es la media de la variable de interés; 
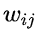es un elemento de una matriz de pesos espaciales con ceros en la diagonal; 
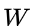es la suma de todos los elementos de la matriz de pesos, es decir:
.
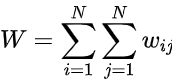La matriz de pesos formada por el conjunto de 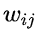se puede definir siguiendo el movimiento de las torres del ajedrez (rook en inglés), o bien siguiendo el movimiento de la reina del ajedrez (queen en inglés). En ambos casos la matriz asigna un peso 1 a las celdas vecinas en las direcciones norte, sur, este y oeste. En el primer caso se asigna un peso 0 a las demás direcciones (diagonales), mientras que en el segundo caso se asigna un peso 0.70711 (=0.5·√2) a las demás direcciones.
La autocorrelación espacial permite identificar patrones espaciales distintos de patrones puramente aleatorios y de patrones regulares, como un tablero de ajedrez. En el ejemplo del tablero de ajedrez, y aplicando el criterio de pesos de 4 vecinos en cruz, el índice obtenido tiene un valor -1; en cambio si los cuadrados blanco del ajedrez se apilan en una mitad del tablero y los negros a la otra, el índice se acerca a +1 a medida que N aumenta; finalmente, en una disposición aleatoria del ajedrez el índice devuelto será un valor cercano a 0. Valores menores que -1 o mayores que +1 son posibles, pero habitualmente corresponden a situaciones muy sesgadas del histograma y con algunos valores que tienen muy pocos vecinos en relación con la distancia analizada.
Para más información se puede consultar la siguiente referencia:
Goodchild, M.F. (1986) Spatial Autocorrelation. Concepts and Techniques in Modern Geography (CATMOG) n. 47, Geo Books, Norwich. 56 p. https://alexsingleton.files.wordpress.com/2014/09/47-spatial-aurocorrelation.pdf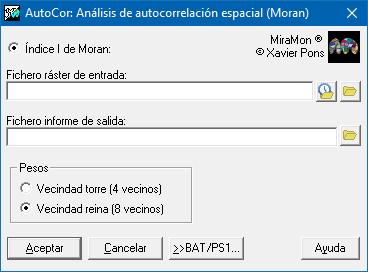
 |
| Caja de diálogo de AutoCor |