-
 RegLog: Regresión logística
RegLog: Regresión logística
Acceso a este texto de ayuda como página web: RegLog
Presentación y opciones
Esta aplicación permite generar un modelo explicativo y predictivo de una variable espacial dicotómica Y en función de n variables espaciales independientes Xn cuantitativas.
La variable dependiente Y siempre será dicotómica y, por tanto, los valores numéricos que tomará serán 1 o 0 (presencia/ausencia, sí/no, éxito/fracaso...). El propósito del análisis es predecir la probabilidad de que la variable Y tome valor 1 en función de los valores de las variables explicativas, P(Y=1|X ), y evaluar la relación o efecto de éstas sobre la variable dependiente.
El análisis está fundamentado en el modelo de regresión logística binaria multivariante que asume que la probabilidad de que la variable Y tome valor 1 sigue la distribución logística y, por tanto, su valor puede ser estimado según la siguiente fórmula, denominada función logística:
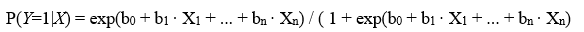
dónde:
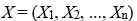 son las variables independientes,
son las variables independientes,
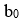 es la constante del modelo o término independente,
es la constante del modelo o término independente,
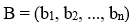 son los coeficientes de las variables independentes.
son los coeficientes de las variables independentes.
Esta función es continua y toma valores en el rango [0,1].
El vector de coeficientes 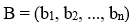 se estima mediante el método de máxima verosimilitud, es decir, los coeficientes son ajustados de forma que se maximiza la función de verosimilitud.
se estima mediante el método de máxima verosimilitud, es decir, los coeficientes son ajustados de forma que se maximiza la función de verosimilitud.
Dado que una variable dependiente dicotómica sigue una distribución binomial, la función de verosimilitud para una muestra aleatoria de N observaciones se expresa por:
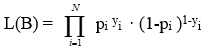
dónde:
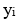 es el valor observado (1 o 0) de la variable dependiente por la muestra i
es el valor observado (1 o 0) de la variable dependiente por la muestra i
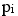 es el valor predicho de la variable dependiente por la muestra i,
es el valor predicho de la variable dependiente por la muestra i, 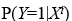 .
.
Los coeficientes que maximicen L(B) también maximizarán su transformación logarítmica. Para maximizar el logaritmo de la función de verosimilitud es necesario encontrar la solución del siguiente sistema de ecuaciones no lineales:
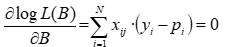
dónde:
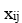 es el valor observado de la variable independiente
es el valor observado de la variable independiente 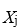 para la muestra i.
para la muestra i.
En la aplicación se ha implementado el algoritmo iterativo de Newton-Raphson para resolverlo.
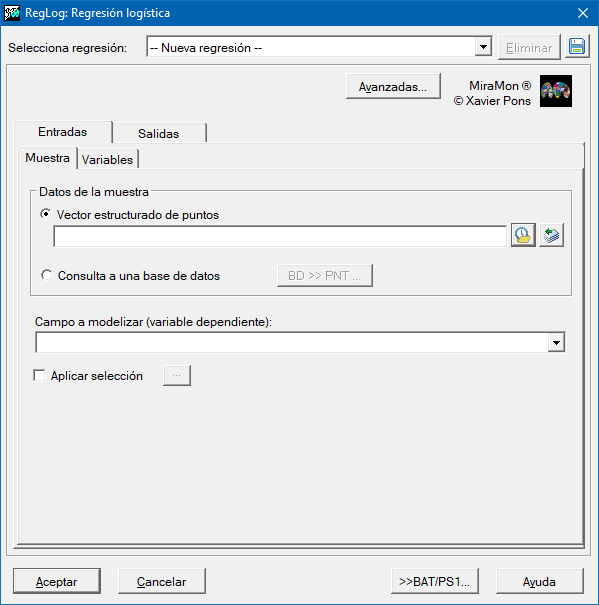
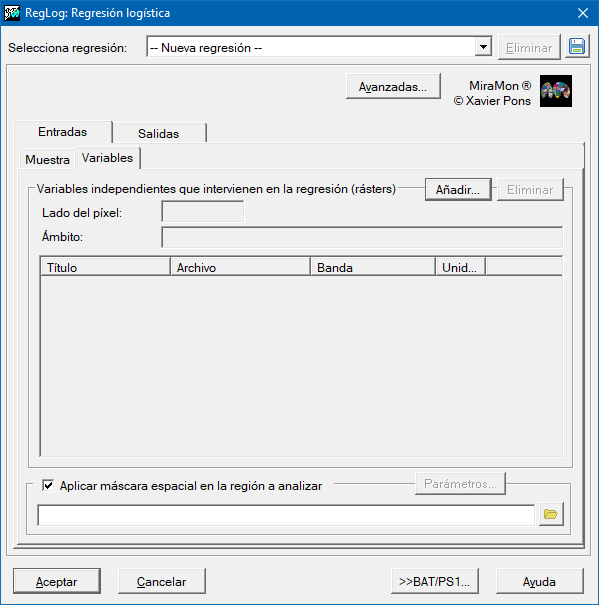
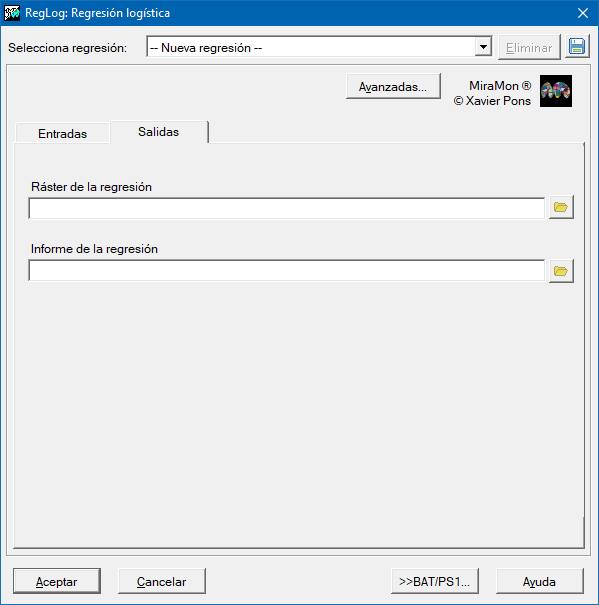
Así pues, para determinar los coeficientes de la regresión es necesario proporcionar un conjunto de muestras en las que es conocida tanto la variable dependiente (1 o 0) en localizaciones concretas (puntuales) como el conjunto de las posibles variables independientes. Estas muestras se proporcionarán en un archivo de puntos estructurado PNT o en una tabla en formato DBF o bien en una tabla en cualquier otro formato accesibles mediante un driver ODBC (Open DataBase Connectivity). Las variables independientes tendrán que ser proporcionadas como rásters en formato IMG del mismo ámbito geográfico y lado de píxel. El resultado predictivo será también un ráster en formato IMG.
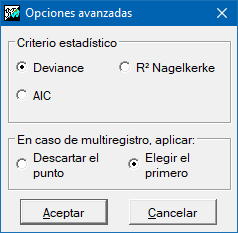
El procedimiento de regresión es, de hecho, un proceso iterativo de ajuste de todas las regresiones posibles: desde la regresión con todas las variables independientes inicialmente introducidas hasta las regresiones con una única variable independiente. Analizando los parámetros estadísticos de cada regresión y en función del criterio escogido (menor coeficiente AIC, menor estadístico Deviance o mejor coeficiente R2 de Naglekerke, se obtiene la que se considera es la mejor regresión de todas.
Para más información del modelo de regresión logística, del método de máxima verosimilitud y del algoritmo iterativo Newton-Raphson se puede consultar la siguiente referencia:
Czepiel, S.A. (2002) Maximum Likelihood Estimation of Logistic Regression Models: Theory and Implementation https://czep.net/stat/mlelr.pdf.

Caja de diálogo de la aplicación
|
| Caja de diálogo de RegLog |

Sintaxis
Sintaxis:
- RegLog Ajuste FichMuestra CampoModel Criterio Multiregistro MDTSalida TXTSalida FichVarIndep [/MOSTRA_VALORS_CRITERIS] [/CAMPY] [/MASCARA] [/CAMP_MASC] [/TAULA_MASC] [/OPER_MASC] [/CONSIDER_NODATA] [/CAMPX] [/REFSYSTEM] /ATR_MASC /PNTdeBD
Parámetros:
- Ajuste
(Opción ajuste -
Parámetro de entrada): Actualmente exclusivamente puede valer 2.
- FichMuestra
(Fichero de entrada de la muestra -
Parámetro de entrada): Fichero de entrada correspondiente a los datos de la muestra.
- CampoModel
(Campo a modelizar (variable dependiente) -
Parámetro de entrada): Campo a modelizar (variable dependiente)
- Criterio
(Criterio estadístico -
Parámetro de entrada):
- 0: Todas las variables son independientes
- 1: Criterio Deviance
- 2: Criterio R2 Naglekerke
- 3: Criterio AIC
- Multiregistro
(Multiregistro -
Parámetro de entrada): Cómo tratar los datos de entrada con multiregistro, es decir, qué hacer cuando se dispone de más de un registro para cada punto:
- 0: Omite el punto.
- 1: Escoger el primero.
- 2: Calcular el promedio de los valores.
- 3: Calcular el sumatorio de los valores.
- MDTSalida
(Fichero MDT de salida -
Parámetro de salida): Fichero MDT de salida
- TXTSalida
(Fichero TXT de salida -
Parámetro de salida): Fichero TXT de salida
- FichVarIndep
(Ficheros de las variables independientes -
Parámetro de entrada): Ficheros de las variables independientes
Modificadores:
/MOSTRA_VALORS_CRITERIS
(Muestra valores y criterios)
Muestra en pantalla información de cada regresión. (Parámetro de entrada) /CAMPY=
(Campo seleccionado de las coordenadas Y)
En caso de pedir la creación de un fichero de puntos a partir de la base de datos de la muestra, es el campo seleccionado de las coordenadas Y. (Parámetro de entrada) /MASCARA=
(Fichero máscara)
Fichero máscara (Parámetro de entrada) /CAMP_MASC
(Campo de la base de datos escogida)
Cuando la máscara es un fichero estructurado, indica el campo de la base de datos escogida. Para saber más sobre los valores de este parámetro se puede consultar las consideraciones del documento de sintaxis general. (Parámetro de entrada) /TAULA_MASC=
(Tabla de la base de datos escogida)
Cuando la máscara es un fichero estructurado, indica la tabla de la base de datos escogida. Para saber más sobre los valores de este parámetro se puede consultar las consideraciones del documento de sintaxis general. (Parámetro de entrada) /OPER_MASC=
(Operador de la proyección del campo)
Operador de la proyección del campo. Exclusivamente en caso de que el archivo máscara sea un archivo de polígonos no estructurado. (Parámetro de entrada) /CONSIDER_NODATA
(Valor sindatos en máscara)
En el caso de un fichero máscara, considerar el valor sindatos. (Parámetro de entrada) /CAMPX=
(Campo de las coordenadas X)
En caso de pedir la creación de un fichero de puntos a partir de la base de datos de la muestra, es el campo seleccionado de las coordenadas X. (Parámetro de entrada) /REFSYSTEM
(Sistema de referencia horizontal del fichero PNT de la base de datos)
En caso de que se pida crear un fichero PNT a partir de la base de datos de la muestra, es el sistema de referencia seleccionado por ese fichero. (Parámetro de entrada) /ATR_MASC=
(Valor seleccionado del fichero máscara)
Valor seleccionado del archivo máscara. Exclusivamente en caso de que el fichero máscara sea un archivo de polígonos no estructurado. (Parámetro de entrada) /PNTdeBD=
(Fichero PNT a partir de una base de datos)
En caso de que los datos de la muestra sean el resultado de una consulta en una base de datos, se puede pedir la creación de un fichero de PNT si también están los identificadores /CAMPX y /CAMPY. (Parámetro de salida)

 RegLog: Regresión logística
RegLog: Regresión logística RegLog: Regresión logística
RegLog: Regresión logística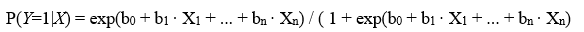
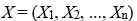 son las variables independientes,
son las variables independientes,
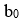 es la constante del modelo o término independente,
es la constante del modelo o término independente,
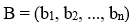 son los coeficientes de las variables independentes.
son los coeficientes de las variables independentes.
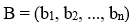 se estima mediante el método de máxima verosimilitud, es decir, los coeficientes son ajustados de forma que se maximiza la función de verosimilitud.
se estima mediante el método de máxima verosimilitud, es decir, los coeficientes son ajustados de forma que se maximiza la función de verosimilitud.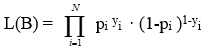
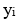 es el valor observado (1 o 0) de la variable dependiente por la muestra i
es el valor observado (1 o 0) de la variable dependiente por la muestra i
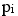 es el valor predicho de la variable dependiente por la muestra i,
es el valor predicho de la variable dependiente por la muestra i, 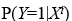 .
.
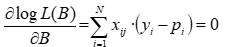
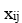 es el valor observado de la variable independiente
es el valor observado de la variable independiente 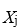 para la muestra i.
para la muestra i.