wVargram: Representaciķ i modelitzaciķ del variogramawVargram: Representaciķ i modelitzaciķ del variogramawVargram és l'eina del MiraMon que representa i modelitza l'anomenat semivariograma, patrķ espacial que descriu la correspondčncia entre la semivariāncia i la distāncia. La semivariāncia, meitat de la variancia, constitueix una mesura de la dispersiķ de la variable respecte el seu valor esperat i es calcula com la suma dels quadrats de les desviacions respecte la mitjana. El semivariograma (o variograma de forma més general i conceptualment equivalents) permet analitzar el comportament espacial d'una propietat o variable sobre la zona d'estudi i la seva modelitzaciķ constitueix un element clau dins procés d'interpolaciķ geostadística (kriging).
La funcionalitat essencial d'aquest mōdul és construir i analitzar el variograma empíric i modelitzar-lo, mitjanįant la generaciķ del variograma ajustat com a possible suma d'alguns dels variogrames elementals implementats: nugget, esfčric, quadrātic, lineal, gaussiā i exponencial. La variable a modelitzar s'introdueix en la modelitzaciķ com un camp específic de la base de dades associada al fitxer estructurat de punts (PNT) i el variograma modelitzat es pot desar com a fitxer ASCII, en format VAM.
La construcciķ del variograma consta de dues etapes organitzades com a dues pestanyes en la interficie del wVargram.
En la primera etapa es fixen les propietats de la mostra de punts i es defineixen els parāmetres geomčtrics i grāfics del Variograma empíric:
Cal, en primer lloc, definir el fitxer de punts corresponent a la mostra de dades a analitzar. Si és necessari, és possible realitzar una selecciķ sobre el conjunt de dades i en aquest cas només intervindran en el procés els punts seleccionats. També cal escollir el camp de la base de dades que conté la informaciķ de la variable a representar i/o modelitzar.
Cal especificar un fitxer per a escriure l'informe de resultats, fitxer de text amb informaciķ sobre el fitxer origen, els parāmetres geomčtrics i grāfics i una llista d'intervals amb el nombre de parelles de punts que pertanyen a cada interval i la mitjana i semivariāncia assignades a l'interval.
Els parāmetres geomčtrics i grāfics a definir sķn els següents (si es necessita determinar la māxima distāncia entre punts es pot solˇlicitar en qualsevol moment amb el botķ "Calcula el m&agr ave;xim"):
Per defecte el sistema realitza els cālculs amb 10 intervals i un 50% de
tall, valors per defecte que es poden recuperar en qualsevol moment en
prémer el botķ corresponent.
També pot ser útil usar el botķ d'actualitzaciķ de parāmetres per a
cončixer com repercuteix en la resta de parāmetres el canvi en un
d'ells.
L'últim pas d'aquesta primera etapa (una vegada estabilitzats els parāmetres ajustables) consisteix a Generar el variograma empíric. Aquest representa un punt per a cada interval en una grāfica on horitzontalment es mostren les distāncies i verticalment la semivariāncia de les parelles de punts que s'han assignat a l'interval corresponent. Consultant a la base de dades alfanumčrica dels punts, s'obtenen els valors específics de la la mitjana i la semivariāncia, per tant amb una precisiķ forįa superior a que es pugui observar grāficament. Aquesta grāfica té 3 nivells de visualitzaciķ:
En resum, aquesta primera parametritzaciķ dķna lloc, i és un dels seus principals objectius, al variograma empíric.
La segona etapa té com a prinicpal objectiu generar el variograma modelitzat i alhora determinar els corresponents parāmetres estrucuturals del seu patrķ espacial. En un primer pas, es trien els variogrames elementals amb els seus parāmetres adequats que conjuntament formaran el variograma ajustat compost. El significat grāfic dels parāmetres que defineixen aquest variogrames elementals poden identificar-se en la següent figura:
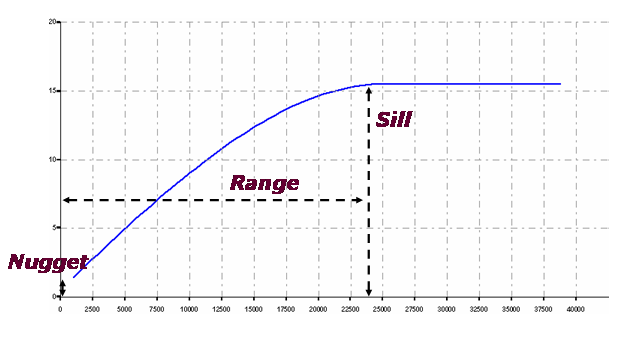
És aconsellable consultar algunes referčncies especialitzades en aquest
punt per a comprendre alguns detalls d'aquesta estructura: dues de
significatives a nivell introductori sķn:
Oliver, M. A., Webster, R. (1990), "Kriging: a method of
interpolation for geographical information systems". International
Journal of Geographical Information Science, 4:3, 313 - 332
Kitanidis P.K. (1997) Introduction to geostatistics: applications
to hydrogeology. Cambridge University Press.
Aquesta segona modelitzaciķ dķna lloc al variograma ajustat o modelitzat, i, si es considera vālid, serā l'usat en mōdul InterPNT per interpolaciķ pel mčtode kriging.
|
|
La primera part de la pestanya de Modelitzaciķ correspon a la construcciķ del variograma ajustat com a suma d'alguns dels variogrames elementals implementats: nugget, esfčric, quadrātic, lineal, gaussiā i exponencial. El fitxer de parāmetres del variograma resultat és un fitxer VAM que es pot carregar a partir d'un fitxer desat a disc o es pot generar de nou i guardar-lo en qualsevol moment. El programa el desa igualment en generar el variograma ajustat.  El directori grāfic del variograma ajustat pot ser un directori temporal, per al cas en que només es vulgui visualitzar la grāfica, o bé un directori específic, per al cas en que es vulgui guardar a disc per a futurs usos. De forma anāloga a la pestanya de lectura de punts i parāmetres es genera una vista prčvia de la grāfica que es pot ampliar fent clic a sobre amb el ratolí i que es genera un grāfic al MiraMon que es pot consultar amb el botķ Obrir grafica al Miramon: |
|
|
|
