| Presentació i opcions | Caixes de diàleg de l'aplicació |
| Exemples gràfics | Sintaxi |
Com en el cas d'altres procediments de càlcul, la interpolació a partir de punts pot donar resultats sensiblement diferents segons les opcions de l'aplicació triades. El mètode triat, la distància llindar, la ponderació a aplicar, la utilització de màscares d'exclusió, etc, poden ajudar enormement a obtenir millors resultats. El coneixement de les dades amb què es treballa i la realització de proves temptatives variant els diferents paràmetres són sovint de gran ajut per a prendre decisions sobre com usar aquests paràmetres. A més a més, per poc que es pugui, convé reservar un conjunt de punts independents aleatòriament distribuïts per tal de poder fer una avaluació quantitativa dels resultats (test).
En els càlculs de quantils, com la mediana, es pot indicar, amb el modificador /MEDIANA_EMPAT=, el tipus de desempat a usar per al seu càlcul quan la posició del quantil sigui entre dos valors de la sèrie. Per a més informació es pot consultar sintaxi general.
En l'actual versió hi ha cinc possibles mètodes d'interpolació: invers de la distància, funció spline, superfícies de tendència, kriging i estadístiques de veïnatge.
Pel mètode de l'invers de la distància, la interpolació del punt problema (cel·la) es realitza assignant pesos als valors dels punts de mostreig en funció inversa de la distància que separa el centre de píxel del punt problema. Aquesta distància pot calcular-se de manera euclidiana, o utilitzant un càlcul simplificat (distància Eixample). Es pot consultar més detalls a https://en.wikipedia.org/wiki/Inverse_distance_weighting.
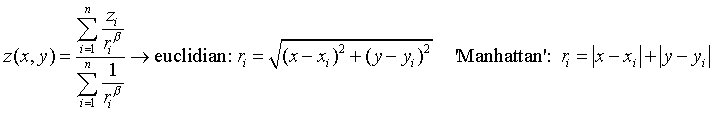
Pel mètode spline es tracta de determinar una funció regular, contínua i derivable, o el conjunt de funcions si dividim l'àmbit global en diferents regions, que s'adapti millor al punts de mostreig sense perdre la seves propietats de continuïtat. Per a conèixer més detalls de l'expressió analítica d'aquesta funció es pot consultar:
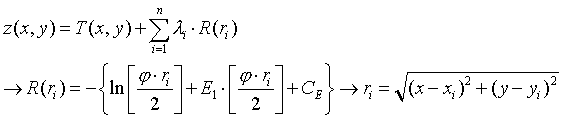
Pel mètode de generació de superfícies de tendència, es tracta d'ajustar una funció polinòmica respecte de les coordenades X, Y de grau 1, 2 o 3 que donarà lloc a una superfície suau, contínua i derivable resultat de l'ajust . Aquest ajust es realitza per mínims quadrats i permetrà determinar els coeficients de cada terme del polinomi.
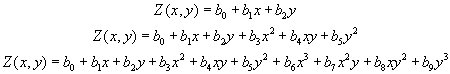
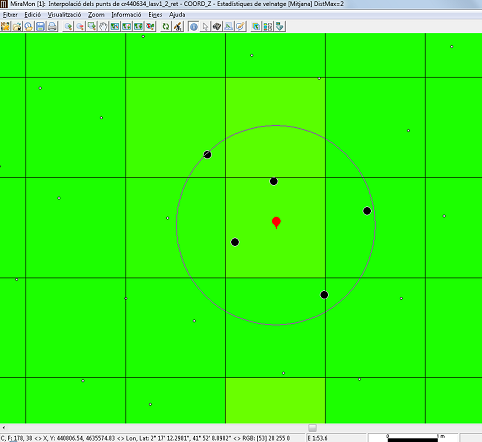
Amb el mètode d'estadístiques de veïnatge, s'assigna a cada cel·la l'estadístic designat (mitjana, mediana, màxim, mínim, rang, desviació estàndard, mitjana de les desviacions absolutes respecte de la mediana o nombre d'ocurrències, percentil), calculat considerant tots els punts que es troben dintre d'un cercle definit per un radi, o dintre d'un quadrat definit per un costat, ubicats al centre de cada cel·la que es vol interpolar. A diferència d'altres mètodes de l'InterPNT, i en particular del mètode que fa la interpolació per ponderació de l'invers de la distància elevada a un exponent determinat per la persona usuària però que també limita aquest càlcul a un cert radi de distància (distància màxima), en el mode d'estadístiques de veïnatge un cop se seleccionen tots els punts presents dintre de l'àmbit (circular o quadrat) indicat, no s'efectua cap ponderació sinó que directament es fa el càlcul demanat, que pot ser una mesura de centralitat dels diferents valors (mitjana o mediana), de dispersió d'aquests valors (màxim, mínim, rang, desviació estàndard, mitjana de les desviacions absolutes respecte de la mediana) o, simplement, un recompte del nombre de valors disponibles (nombre d'ocurrències).
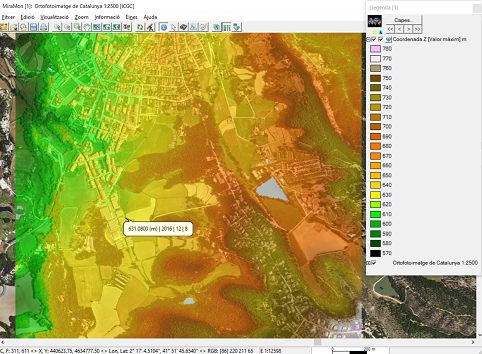
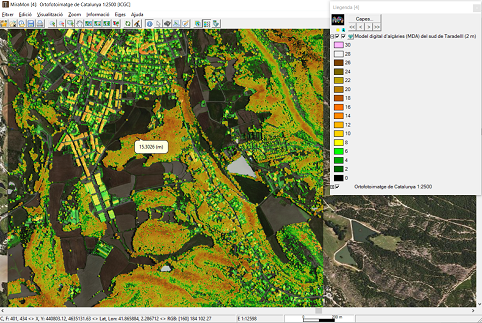
Aquest és un mètode típic per al processament de dades lidar, i particularment per a la producció de Models Digitals de Superfícies (MDS) o de Models Digitals d'Alçàries (MDA). En aquestes dues aplicacions se sol prendre la cota més alta obtinguda pel lidar en l'àmbit de la cel·la del ràster a obtenir. Aquest àmbit pot ser l'àrea de la cel·la si la densitat de punts és prou alta en relació a la grandària de la cel·la, o una mica més gran (per exemple un radi 1.5 cops el costat de la cel·la); es poden consultar les opcions específiques, més avall, per a més detalls.
Si la densitat de punts és molt alta es pot demanar, en comptes del màxim, un percentil 90, etc, amb la qual cosa es redueix la probabilitat d'adoptar com a superfície real algun artefacte del sensor com ara la detecció d'ocells volant en aquell moment. Amb altres estadístiques, com les de dispersió, es poden tenir dades interessants de l'estructura vertical de les masses de vegetació. Finalment, amb l'elecció d'estadístiques de mínim, combinades amb la selecció de punts que corresponguin a retorns únics (informació disponible a un dels camps de la taula d'atributs) i d'intensitats de retorn elevades (dada també disponible a un altre camp), i amb radis d'exploració molt grans (diversos cops el costat de cel·la a obtenir), es pot obtenir un Model Digital d'Elevacions (MDE). Si ja es disposa d'un MDE, o aquest s'ha calculat amb les dades lidar com s'acaba de descriure, es pot obtenir un MDA (les dades altimètriques de la vegetació o de les construccions humanes es mesuren des del terra i no des del nivell del mar); en aquest cas el més pràctic és, abans d'executar l'InterPNT, executar l'aplicació CombiCap en la forma MDE+PNT-->PNT i amb el mode de transferència de camps estadístics utilitzant la interpolació bilineal, on el segon PNT obtindrà les elevacions a cada punt lidar; a continuació es genera un camp buit de tipus numèric i típicament amb 2 o 3 decimals per tal que, amb l'ús de CalcImg, sigui omplert amb l'alçària del punt (calculada fent la resta entre l'altitud obtinguda pel lidar i l'elevació resultant del CombiCap). Aquesta alçària és la que se sotmet a l'InterPNT per a obtenir el MDA.
Operació general
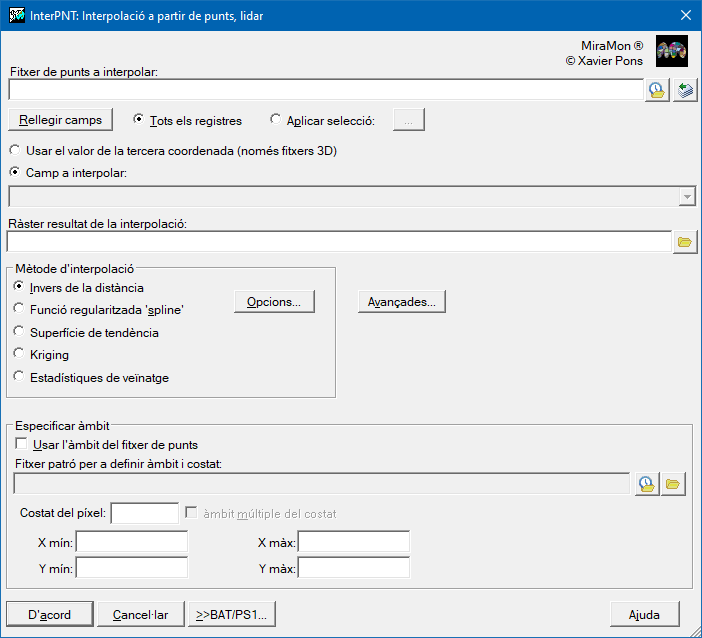
En primer lloc, cal escollir si es vol usar el valor de la tercera coordenada (en el cas de fitxers 3D) o seleccionar un camp a interpolar de la base de dades associada al fitxer de punts. En el cas d'escollir un camp de la base de dades, cal seleccionar un camp numèric. Encara que els valors d'aquest camp puguin ser enters, l'interpolador tractarà aquestes dades com a reals de doble precisió en tots els càlculs interns i generarà un ràster resultat de reals amb precisió simple.
La selecció de registres és el primer filtre que tria aquells registres, de la base de dades del fitxer de punts, que participaran en la interpolació. L'opció per defecte és 'Tots els registres', però en molts casos millorarem la qualitat i la velocitat de la interpolació si excloem aquells registres que no desitgem que tinguin cap influència en el resultat. La selecció de registres es fa en construir una sentència lògica sobre qualsevol combinació de camps de la base de dades associada al fitxer de punts. Noteu que els camps implicats en la selecció poden no involucrar el camp a interpolar. Per exemple, si en un fitxer d'emissions atmosfèriques, un camp indica la comarca on és cada indústria i volem interpolar un cert contaminant, podem indicar que s'interpoli només amb els valors d'una certa comarca. Recomanem utilitzar la finestra que s'obre a partir de l'opció 'Aplicar selecció' per a construir aquesta sentència lògica, a base d'anar seleccionant els camps, operadors, valors, nexes i ordre de prioritats amb els botons i desplegables corresponents. En la secció explicativa de la 'Sintaxi' de la línia de comanda detallem els elements d'aquesta sentència, que funciona de forma semblant a la consulta per atributs de MiraMon.
El fitxer de sortida serà un ràster no comprimit de valors reals (excepte quan es defineixin màscares d'exclusió, que serà comprimit i també de valors reals). Aquest ràster tindrà definit el valor de fons o sensedades en aquelles cel·les on no hagi quedat definit cap valor possible perquè aquella coordenada no verifica els criteris de les 'Opcions avançades', perquè és dintre una màscara d'exclusió o perquè no té un mínim de punts suficients dins la distància màxima d'influència.
Cal definir l'envolupant i costat de píxel d'aquest ràster de sortida, explicitant les coordenades o ajustant l'envolupant a l'àmbit del fitxer de punts. Cal notar que la velocitat del procés és molt sensible a aquests valors. Un costat petit en una regió a interpolar molt àmplia sense màscara definida, donarà uns valors molt precisos (suaument variables en funció de la distància), però el nombre de càlculs serà molt gran i el temps d'execució, llarg.
Opcions per a l'invers de la distància
Cal definir en primer lloc, com es realitzarà el càlcul de la distància; de forma euclidiana o a l'estil 'Eixample' (vegeu en l'apartat anterior, ambdues definicions de distància). El càlcul del valor que s'assignarà a cada cel·la és una mitjana ponderada dels valors que prenen els punts a considerar. El pes que pren cada punt té una dependència potencial respecte l'invers de la distància entre el punt i el centre del píxel. El valor per defecte és 2, però pot parametritzar-se de la manera que l'usuari cregui més adequada. Com més alt és el valor, més pes té el punt en el seu entorn immediat, i menys pes la mitjana dels valors circumdants.
La distància màxima és un paràmetre molt habitual que marca una regió d'influència dels punts localitzats en l'interior d'una circumferència, centrada en el píxel, i de radi igual a la distància màxima indicada. Per tant, per a cada cel·la tindrem una distància a partir de la qual els punts originals no juguen cap paper en el procés d'interpolació. Cal tenir present que és molt raonable usar sempre aquest paràmetre, ja que a més a més de tenir ple sentit en la interpolació, permet reduir extraordinàriament el temps d'execució.
Un altre criteri interessant és definir el nombre màxim de punts del quals dependrà el càlcul. Evidentment sempre seran els 'n' més propers al centre del píxel. Els reiterats processos d'ordenació que requereix l'aplicació d'aquest criteri, fa allargar considerablement el procés de càlcul, però assegurem la intervenció només dels 'n' més propers. Per a assegurar que el càlcul es fa amb un mostreig suficient, també podem definir un nombre mínim de punts a participar en el càlcul de cada cel·la. Si no s'assoleix aquest mínim, el valor de la cel·la serà sensedades.
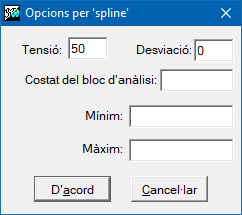
Opcions per a spline
La interpolació per splines pot ser segons la configuració dels punts de mostra, força sensible als paràmetres de configuració.
El paràmetre tensió modula la suavització de la funció; el seu valor per defecte és 40 i tensions excessivament baixes o elevades poden donar lloc a artefactes inesperats.
El paràmetre desviació ajusta el soroll de la mostra, el valor per defecte zero implica que la funció passa exactament pels punts de mostreig (interpolador exacte).
El paràmetre costat de bloc d'anàlisi localitza l'ajust en dividir l'àmbit per blocs d'anàlisi on es restringeix la solució de la funció spline a aquesta regió. Aquest paràmetre accelera força els càlculs, és molt recomanable quan disposem de molts punts, però pot arribar a produir discontinuïtats no desitjades si el seu valor és massa petit (finestra massa local).
El mètode spline es comporta de manera òptima per a mostres sense excessives pertorbacions. Ara bé, si localment es tenen punts propers amb variacions brusques de la variable a interpolar, el mètode pot donar lloc a valors força allunyats del rang esperat. En aquest cas és força recomanable incrementar la tensió i com a opció complementària forçar els valors de sortida dins un màxim o un mínim. En aquest cas cal definir els modificadors /MIN_VAL i /MAX_VAL.
Si no es defineix el costat d'anàlisi, la solució és única per tot l'àmbit (finestra igual a l'àmbit), si el costat d'anàlisi és petit, l'àmbit es dividirà en moltes regions independents.
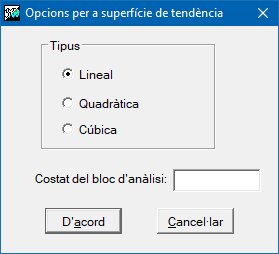
Opcions per a les superfícies de tendència
El principal paràmetre d'aquesta opció és el grau que determina l'ordre del polinomi a ajustar. En l'actual versió és possible generar superfícies de primer grau o lineals, de segon grau o quadràtiques i de tercer grau o cúbiques.
De la mateixa manera que per spline, és possible generar diferents solucions, no estrictament contínues, en dividir l'àmbit global en subregions més locals. Aquestes subregions queden definides pel paràmetre costat de bloc d'anàlisis.
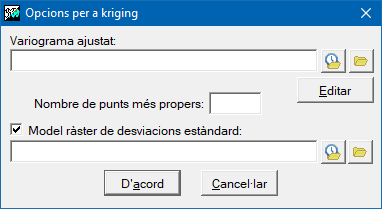
Opcions per al kriging
El mètode d'interpolació kriging està basat en els principis de la geoestadística. Per tal de poder-lo aplicar, cal prèviament haver generat un fitxer del variograma ajustat (amb extensió "vam"). Aquest fitxer es pot generar amb l'aplicació Vargram, a l'ajuda de la qual trobareu indicacions sobre com modelitzar el patró espacial de la variable a analitzar que dóna lloc al variograma que s'aplicarà per a la interpolació amb aquest mètode. En les opcions avançades de l'InterPNT, es pot limitar el nombre de punts més propers a cada cel·la que participen en el seu valor resultant, així com obtenir un ràster auxiliar de la qualitat de la estimació, on s'emmagatzemaran les desviacions estàndard per a cada cel·la. Es pot ampliar informació sobre el kriging a https://en.wikipedia.org/wiki/Kriging. En català s'ha proposat el mot krigatge per a aquest mètode.
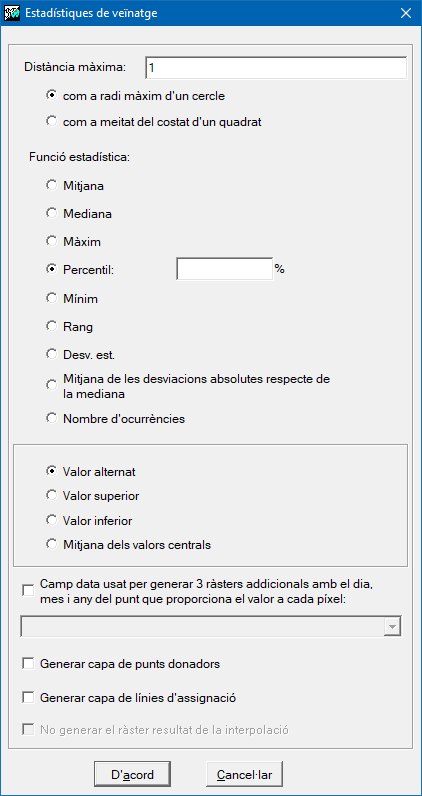
Opcions per a les estadístiques de veïnatge
Cal definir dos paràmetres: la funció estadística a utilitzar, i la distància màxima a la qual un punt es considera que ha de formar part del conjunt de punts que proporcionen els valors per al càlcul de l'estadístic que es transferirà a la cel·la del ràster de sortida.
Les funcions estadístiques disponibles són la mitjana, la mediana, el màxim, el mínim, el rang, la desviació estàndard, la mitjana de les desviacions absolutes respecte de la mediana i el nombre d'ocurrències.
Per a la distància màxima hi ha dues opcions possibles: distància màxima com a radi màxim d'un cercle, i distància màxima com a meitat del costat d'un quadrat. Aquesta darrera opció és típicament utilitzada quan es vol que els punts lidar amb els quals es calcularà el valor de l'estadístic que s'escriurà a la cel·la estan ubicats estrictament al seu interior; cal notar que, com que la dada és la meitat del quadrat, si s'ha indicat que es vol obtenir un ràster de 2 m de costat, la distància a indicar per a la distància màxima serà 1 m. Quan el valor de l'estadístic calculat prové d'un sol punt, com en el cas del mínim i el màxim, és possible obtenir capes addicionals (de nom igual a la capa de sortida i amb un sufix apropiat): D'una banda, si les dades lidar proporcionen, en sengles camps, el dia, mes i any de captura de cada punt és possible generar 3 ràsters addicionals que contindran el dia, mes i any del punt que proporciona el valor a cada píxel. D'altra banda, i per a propòsits didàctics i de recerca, és possible generar capes addicionals que continguin només els punts donadors, o que uneixin amb línies els punts donadors amb el centre de la cel·la receptora del valor.
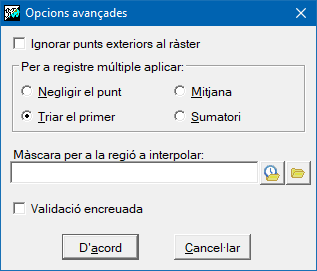
Opcions avançades
Les opcions avançades ens permeten parametritzar de la forma més ajustada possible alguns procediments globals de la interpolació.
En el cas que a un punt hi tinguem associat més d'un registre seleccionat (p.ex. diverses mesures en instants diferents d'una mateixa font), podem triar com serà el valor a interpolar en aquest punt. a) negligir aquest punt amb registre múltiple (per tant, serà com si no formés part de la selecció); b) triar el valor del primer registre que verifiqui les condicions de selecció; c) fer una mitjana entre aquests registres; d)fer una suma.
Una possibilitat afegida és la tria de punts de manera que s'ignoren aquells punts exteriors a l'envolupant definida pel ràster. Aquest opció no es recomana si els valors propers a les vores del ràster de sortida són importants.
Finalment, també podem determinar sobre quines regions dins l'àmbit definit, no necessitem o no desitgem conèixer el resultat de la interpolació. Utilitzant un fitxer que actuï de màscara d'exclusió i determini quines zones són útils i quines no, accelerarem considerablement el procés de càlcul, i obtindrem resultats més coherents per exclusió de zones sense punts; per exemple, si estem interpolant elevacions terrestres a partir de cotes, podem excloure de la interpolació totes les zones marítimes). Aquesta màscara pot ser un ràster on les regions a excloure seran aquelles en què el valor de la cel·la és sensedades. També pot ser un vector, estructurat o no estructurat, però sempre de tipus polígon. En aquest cas la zona a excloure serà per defecte el polígon universal, o bé la màscara inclourà aquells polígons amb atribut igual o diferent a un valor determinat si es defineix expressament. Per a vectors estructurats cal, a més a més, concretar quin camp de la taula d'atributs definirà la màscara.
 |
|||
 |
 |
 |
 |
 |
|||
 |
|||
| Caixes de diàleg de l'InterPNT | |||