-
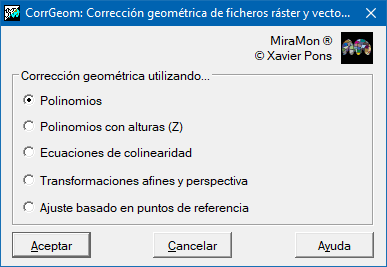
 CorrGeom: Corrección geométrica de ficheros ráster y vectoriales
CorrGeom: Corrección geométrica de ficheros ráster y vectoriales
Acceso directo de la ayuda en Internet: CorrGeom
Acceso a la aplicación desde el menú:
"Herramientas | Geometría | Correcciones elementales (traslación, rotación, etc)"
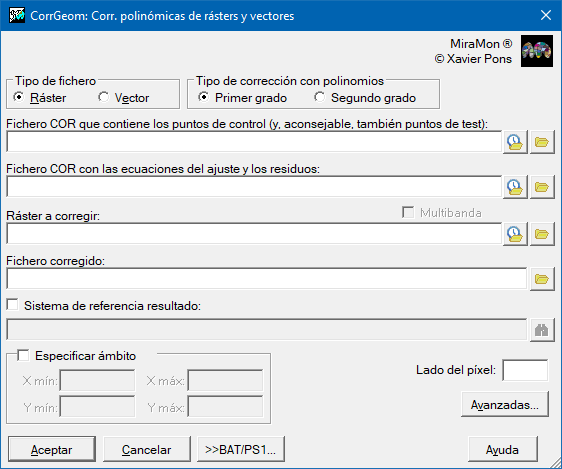
"Herramientas | Geometría | Correcciones polinómicas de rásters y vectores"
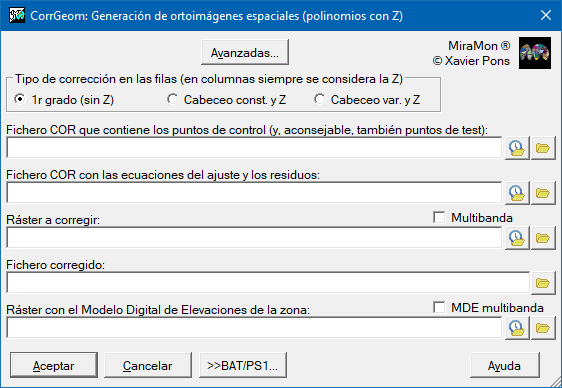
"Herramientas | Geometría | Generación de ortoimágenes espaciales"
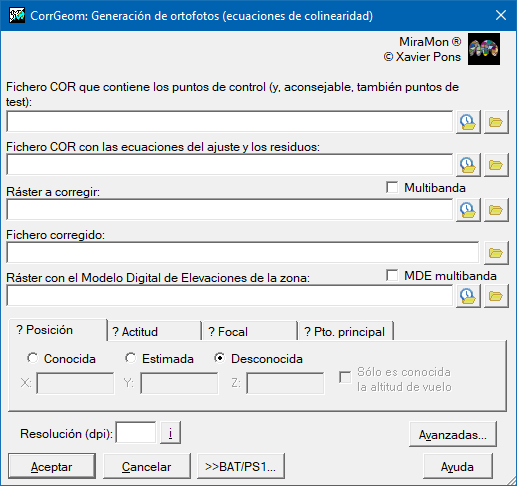
"Herramientas | Geometría | Generación de ortofotos"
Presentación y opciones
Introducción
La cartografía convencional sobre papel nos ofrece una enorme fuente de información para incorporar en el seno de un Sistema de Información Geográfica (SIG). Aunque cada vez más la cartografía se genera digitalmente en su origen, todavía existen muchos casos en los que no disponemos de los ficheros digitales, ya sea porque se trata de documentos con cierta antigüedad, o bien porque se han elaborado con técnicas analógicas convencionales , o simplemente porque no tenemos acceso a la información digital original.
En estos casos, aunque la digitalización en tabla es una posibilidad factible, representa un esfuerzo pesado y una pérdida de detalle respecto a la posibilidad de escanear el documento analógico y proceder a su digitalización sobre la pantalla del ordenador.
MiraMon permite transformar ficheros procedentes de prácticamente cualquier escáner (formatos BMP, TIFF, JPG, etc) a formato IMG o JPG (si no lo eran en su origen). Una vez en este formato podremos digitalizar encima las curvas de nivel, carreteras, polígonos de usos del suelo, etc y convertirlos en capas vectoriales. Asimismo, los documentos escaneados no están todavía georeferenciados, con lo cual si digitalizamos directamente encima, las coordenadas de los vectores resultantes estarán en unidades arbitrarias (píxels) del sistema de escaneo y no en unidades mapa del sistema de destino (por ejemplo en metros del sistema UTM). Aunque es posible proceder así y georeferenciar posteriormente el documento vectorial resultante con el programa CorrGeom de MiraMon, resulta aconsejable georeferenciar el ráster y proceder posteriormente a su digitalización, ya que si escaneamos la hoja a trozos podrán mosaicarse con precisión los resultados y, además, en cualquier momento podemos superponer al documento escaneado otras capas de información vectorial de las que disponemos para que nos sirvan de referencia. La georeferenciación de los rásters escaneados también se efectúa desde el programa CorrGeom de MiraMon. En resumen, por tanto, tenemos dos alternativas para la introducción en nuestro SIG de capas vectoriales a partir de documentos en papel escaneados y el programa CorrGeom de MiraMon:
- Escaneado -> Digitalización -> Georeferenciación de los vectores
- Escaneado -> Georeferenciación del ráster ->Digitalización (ACONSEJADO)
En ambos casos el método recomendado es el ajuste polinómico de primer grado. En el caso muy improbable con los escáners modernos, de que la imagen escaneada presente deformaciones cuadráticas, utilice un ajuste polinómico de segundo grado.
Por otra parte, existen otras fuentes de información muy interesantes para incorporar en nuestro SIG: se trata de capas ráster como las imágenes de teledetección y las fotografías aéreas. Estos materiales pueden obtenerse directamente en formato digital (en el caso de la mayoría de imágenes de teledetección) o bien, si vienen sobre un soporte de papel o fotográfico (en caso de fotografías aéreas convencionales), pueden escanearse para convertirlas en una imagen digital.
Las imágenes de teledetección presentan una serie de deformaciones geométricas producidas por la rotación y curvatura de la Tierra, la órbita de la plataforma, etc. El programa CorrGeom de MiraMon permite corregir estas imágenes mediante las técnicas convencionales basadas en polinomios de primero y segundo grado. En el caso de las fotografías aéreas y de las imágenes de teledetección con cierto detalle (píxel de 50 m o menor) es aconsejable efectuar la corrección teniendo en cuenta el relieve terrestre. CorrGeom ofrece los métodos "ajuste polinómico con zetas" para imágenes de satélite con tamaños de píxel pequeños (Landsat TM, SPOT XS y P, IRS LISS, etc) y "ajuste mediante ecuaciones de colinealidad" para fotografía aérea, método que aplica las ecuaciones fundamentales de la fotogrametría. Estas imágenes corregidas geométricamente utilizando el relieve a través de un Modelo Digital de Elevaciones (MDE) reciben el nombre de ortoimágenes (ortofotos en el caso de fotografía aérea).
El programa CorrGeom, por tanto, permite corregir estas deformaciones (órbita de las plataformas, relieve terrestre, etc) y adaptar las imágenes a un sistema de proyección cartográfica conocido, como por ejemplo UTM. Una vez en el sistema de proyección adecuado, las imágenes podrán superponerse con otras imágenes y capas vectoriales en el mismo sistema de proyección.
Tanto para corregir rásters como vectores habitualmente hay que disponer de un conjunto de puntos de control sobre el terreno (GCP) los cuales nos indican diversas coordenadas en el sistema de referencia origen (no corregido) y destino (corregido). Los GCP pueden entrarse con un editor de textos o pueden digitalizarse con MiraMon como puntos y convertirlos en GCP con VECCOR (ver más abajo).
En el caso de imágenes captadas desde un sistema que conozca con exactitud suficiente la posición y actitud del sensor (GPS+INS) se puede llegar a hacer la corrección sin GCP.
Para una mayor fiabilidad estadística del proceso de corrección geométrica, CorrGeom permite que el fichero de puntos de control contenga dos subconjuntos de puntos, uno que se utiliza para efectuar los ajustes de las ecuaciones de corrección, y otro, al que llamamos puntos de test, que se utiliza para estimar el error con un conjunto independiente de puntos. Para ambos conjuntos de puntos, CorrGeom proporciona el error RMS en X, Y y global para cada punto así como para el conjunto de puntos de control. Lógicamente, si solamente se dan puntos de ajuste solamente se proporcionan estos RMS para el conjunto de puntos del ajuste.
Si desea cambiar el sistema de proyección de rásters o vectores, una vez georeferenciados con MiraMon (o ya georeferenciados en origen e importados a MiraMon), utilice el programa CanviPrj. No confunda, pues, la funcionalidad de CorrGeom que permite georeferenciar una capa no georeferenciada con CanviPrj que permite reproyectar una capa de la que ya conocemos la georeferenciación.
NOTAS:
- Cuando hablemos de sistema de proyección nos referiremos a UTM, Lambert, etc, mientras que cuando hablemos de sistema de referencia nos referiremos a UTM-31N-UB/ICC (UTM en el huso 31, hemisferio Norte, datum europeo ED50 con parámetros ajustados para UB/ICC), o Goode_Homolosine-WGS84 (Goode Homolosine WGS84 con datum WGS 1984), etc. (vea la ayuda Geodesia para más información)
- En adelante nos referiremos a las imágenes y vectores que han sido adaptados a algún sistema de referencia utilizando CorrGeom como "corregidos".
CorrGeom
Este programa permite corregir geométricamente rásters (IMG y JPG: imágenes de satélite, fotografía aérea, mapas escaneados...) o capas vectoriales (VEC, PNT, ARC y sus derivados POL y NOD) a partir de n puntos de control de los cuales se conoce:
- Coordenadas en el sistema de referencia origen (sistema "no corregido"), p.ej. en unidades píxel, con origen típicamente (0,0) en el vértice inferior izquierdo- en los rásters, o p. ej. en cm en un fichero proveniente de una digitalización vectorial de un mapa de papel efectuada sobre una tabla digitalizadora calibrada a unidades cm de papel. Llamaremos a estas coordenadas, coordenadas en el sistema de referencia origen: X_SistOri, Y_SistOri.
- Coordenadas en el sistema de referencia escogido (sistema "corregido" o "mapa", como por ejemplo UTM-31N). Estas coordenadas se determinan manualmente con la ayuda de mapas de papel, sobre la pantalla con otros mapas digitales, con GPS sobre el terreno, etc. Llamaremos a estas coordenadas, coordenadas en el sistema de referencia destino: X_SistDest, Y_SistDest [, Z_SistDest].
Además, el programa permite aplicar transformaciones afines (translaciones, rotaciones, inclinaciones, escalados y reflejos) y una perspectiva tanto en rásters como en vectores.
En caso de que desee corregir todas las bandas de un ráster multibanda (típicamente una RGB de 24 bits o una imagen satélite multiespectral) puede indicarle al programa, con el parámetro /MULTIBANDA o activando el botón correspondiente que las corrija todas en una sola ejecución y el resultado continuará siendo un ráster multibanda. En este caso, aconsejamos editar los puntos de control sobre la banda con mayor resolución. Si la corrección requiere el modelo digital de elevaciones (MDE), en el caso de que las diferentes bandas a corregir tengan diferentes lados de píxel, podemos utilizar un MDE multibanda con tantas bandas como diferentes lados de píxel activando el parámetro /MDE_MULTIBANDA.
Se puede efectuar la corrección mediante diferentes métodos:
Ajuste polinómico de primer grado (caso ráster):
En este caso, el método no considera las zetas (elevaciones). Típico para corregir ficheros rásters con poca deformación, como imágenes, y mapas escaneados ya corregidos (como ortofotos o mapas topográficos) o imágenes de satélite de zonas con poco relieve, alcance territorial moderado y píxel relativamente grande con respecto a la altura de vuelo del satélite. La aplicación de estos métodos a fotografías aéreas escaneadas o imágenes de satélite con relativo detalle (como Landsat-TM o SPOT) y extensión solamente es adecuada en zonas de relieve plano y si se quiere obtener cartografía de alta calidad geométrica.
Ajuste polinómico de primer grado (caso vectorial):
En este caso, el método no considera las zetas (elevaciones). Típico para corregir ficheros vectoriales con poca deformación.
Ajuste polinómico de segundo grado (caso ráster):
En este caso, el método no considera las zetas (elevaciones). Típico para corregir ficheros ráster con poca deformación, como imágenes, y mapas escaneados ya corregidos (como ortofotos o mapas topográficos) o imágenes de satélite de zonas con poco relieve, alcance territorial moderado y píxel relativamente grande con respecto a la altura de vuelo del satélite. La aplicación de estos métodos a fotografías aéreas escaneadas o imágenes de satélite con relativo detalle (como Landsat-TM o SPOT) y extensión solamente es adecuada en zonas de relieve plano y si se quiere obtener cartografía de alta calidad geométrica.
Ajuste con polinomio con Z para las columnas y polinomio de 1r grado sin Z para las filas:
En el caso del ajuste con polinomio con Z para las columnas y polinomio de 1r grado sin Z para las filas, el ajuste de las columnas se hace usando un polinomio que tiene en cuenta simultáneamente X, Y y Z. En lo que a filas respecta, el ajuste puede hacerse de tres maneras diferentes: considerando que no hay cabeceo del sensor durante la toma de la imagen, considerando que el cabeceo es constante o, considerando que varía según un modelo lineal. Para más detalle se puede consultar:
Palà, V., Pons, X. (1995) Incorporation of relief into geometric corrections based on polynomials. Photogrammetric Engineering & Remote Sensing, 61(7):935-944.
Ajuste con polinomio con Z para las columnas con cabeceo constante y polinomio de 1r grado con Z para las filas:
En este caso, análogo al anterior pero con cabeceo constante y polinomio de 1r grado con Z para la filas, el ajuste de las columnas se hace usando un polinomio que tiene en cuenta simultáneamente X, Y y Z. En lo que a filas respecta, el ajuste puede hacerse de tres maneras diferentes: considerando que no hay cabeceo del sensor durante la toma de la imagen, considerando que el cabeceo es constante o, considerando que varía según un modelo lineal. Para más detalle se puede consultar:
Palà, V., Pons, X. (1995) Incorporation of relief into geometric corrections based on polynomials. Photogrammetric Engineering & Remote Sensing, 61(7):935-944.
Ajuste con polinomio con Z para las columnas con cabeceo variable y polinomio de 1r grado con Z para las filas:
En este caso, análogo al anterior con cabeceo variable, el ajuste de las columnas se hace usando un polinomio que tiene en cuenta simultáneamente X, Y y Z. En lo que a filas respecta, el ajuste puede hacerse de tres maneras diferentes: considerando que no hay cabeceo del sensor durante la toma de la imagen, considerando que el cabeceo es constante o, considerando que varía según un modelo lineal. Para más detalle se puede consultar:
Palà, V., Pons, X. (1995) Incorporation of relief into geometric corrections based on polynomials. Photogrammetric Engineering & Remote Sensing, 61(7):935-944.
Ajuste mediante ecuaciones de colinealidad:
Los parámetros implicados en las ecuaciones de colinealidad son: posición (Xc, Yc, Zc) y actitud (omega, fi, kappa) de la cámara o sensor, focal de la cámara (f) y coordenadas del punto principal (x_pp, y_pp) de la imagen. De estos parámetros, el usuario puede decidir cuáles ajustar y cuáles vienen fijados. Sobre los que hay que ajustar, es útil dar unos parámetros estimados que ayuden al programa a converger más rápidamente. En algún caso, si el parámetro inicial es completamente desconocido o la estimación es poco adecuada, puede ser que el sistema no converja hacia ninguna solución o que encuentre unas soluciones poco satisfactorias. Si se conocen y fijan todos los parámetros, se aplica la transformación sin tener en cuenta los puntos de control y usando los puntos de test para evaluar el error en el ajuste. Estos son los valores iniciales de los parámetros de vuelo en la primera iteración: - Aleteo: omega = 0
- Cabeceo: fi = 0
- Deriva: kappa = Se prueban diferentes valores y se toma el que dé un RMS más pequeño en las primeras iteraciones.
- Xc = Media de las coordenadas X (destino) de los puntos de control.
- Yc = Media de las coordenadas Y (destino) de los puntos de control.
- Zc = Zc media + altitud de vuelo, aprox. 2000-3000 m
Cuando hay que ajustar el punto principal (x_pp, y_pp), el programa toma como valores iniciales:- x_pp = Media de las coordenadas x (origen) del punto de control o punto medio del ráster .
- y_pp = Media de las coordenadas y (origen) del punto de control o punto medio del ráster.
Sin embargo, a veces estas medias pueden quedar bastante alejadas del punto principal real y en este caso el programa puede no converger (p.ej. si se escanea solamente un fragmento lateral de una fotografía aérea analógica). El programa ofrece al usuario la posibilidad de cambiar el valor por otro estimado a ojo en el cruce de las marcas fiduciales; tenga en cuenta que debe usar siempre el mismo sistema de medición, coherente con las coordenadas del sistema de referencia origen.
Para el ajuste de la focal, hay que escoger un valor inicial cercano al real, típicamente entre 15 y 35 mm para cámaras digitales y entre 50 y 250 mm para cámaras analógicas.
Adicionalmente habrá que conocer los puntos por pulgada (ppp o dpi) de escaneo de la imagen (1 pulgada = 25.4 mm). En el caso de fotografías analógicas son valores frecuentes entre 400 y 200 dpi. En fotografías digitales convendrá consultar las especificaciones técnicas (por ejemplo la cámara AA497-AMDC 28.0 de 2024 columnas x 2041 filas y tamaño de sensor de 18x18 mm da lugar a una resolución de 2811-2835 dpi).
Transformaciones geométricas (afines y perspectiva) (caso ráster):
Estos tipos de transformaciones siguen una filosofía diferente a las anteriores: en vez de ajustar la transformación mediante puntos de control, el usuario conoce a priori los parámetros de la transformación y por ello debe indicarlos. Así, puede ser que hayamos escaneado un documento rotado 90º porque cabe mejor en el escáner; en este caso será más fácil efectuar una rotación de 90º para volver a ponerlo en la posición original y verlo de forma "natural" (quizás antes de colocar puntos de control para un ajuste fino de la geometría).Un segundo ejemplo sería una base donde las unidades del sistema de referencia horizontal están en km y queremos tenerlas en m, para lo cual aplicaremos uno escalado de valor 1000.
Los tipos de operaciones que se ofrecen son: translaciones, escalados, inclinaciones, rotaciones, perspectivas y reflejos. Para las transformaciones afines (todas menos la perspectiva) se puede especificar un origen de transformación y para la perspectiva se puede especificar un envolvente sobre el cual actuar. Se da la posibilidad de escogerlo porque si se quiere modificar una capa vectorial sobre un ráster ya modificado, se pueda usar el envolvente del ráster y superponer así perfectamente la capa vectorial transformada sobre el ráster modificado.
Es posible realizar una serie de transformaciones y/o perspectiva una detrás de la otra sobre un ràster o vector con la única restricción de que sólo se puede usar una perspectiva.
Transformaciones geométricas (afines y perspectiva) (caso vectorial):
Estos tipos de transformaciones siguen una filosofía diferente a las anteriores: en vez de ajustar la transformación mediante puntos de control, el usuario conoce a priori los parámetros de la transformación y por ello debe indicarlos. Un ejemplo sería el caso de una base vectorial antigua, proveniente de un software que almacenaba las coordenadas con precisión simple (como PC-Arc/Info) y se había truncado la cifra más significativa cuando era constante para toda la capa (por ejemplo en Cataluña en UTM-31N era habitual suprimir el 4 de la coordenada Y, por lo cual una coordenada como 4619254.734 se escribía 619254.734 y así se podía mantener una precisión decimétrica; en este caso podremos recuperar las coordenadas originales indicando una transformación de tipo translación de magnitud 4000000. Finalmente, un tercer ejemplo sería una base donde las unidades del sistema de referencia horizontal están en km y queremos tenerlas en m, para lo cual aplicaremos uno escalado de valor 1000.
Los tipos de operaciones que se ofrecen son: translaciones, escalados, inclinaciones, rotaciones, perspectivas y reflejos. Para las transformaciones afines (todas menos la perspectiva) se puede especificar un origen de transformación y para la perspectiva se puede especificar un envolvente sobre el cual actuar. Se da la posibilidad de escogerlo porque si se quiere modificar una capa vectorial sobre un ráster ya modificado, se pueda usar el envolvente del ráster y superponer así perfectamente la capa vectorial transformada sobre el ráster modificado.
Es posible realizar una serie de transformaciones y/o perspectiva una detrás de la otra sobre un ràster o vector con la única restricción de que sólo se puede usar una perspectiva.
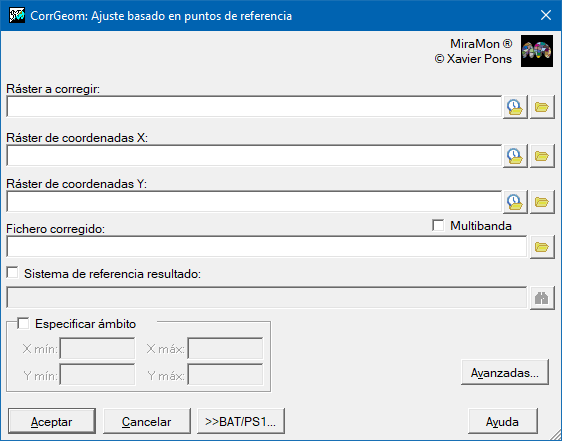
Ajuste basado en puntos de referencia:
En este caso, la corrección geométrica se realiza a partir de dos rásters que, emparejados, proporcionan la posición origen de cada píxel de la imagen destino (por tanto, típicamente tienen las mismas dimensiones que ésta) y conjuntamente forman, pues, una malla de referencia.
El procedimiento se basa en lo siguiente: Para cada centro de píxel del ráster de salida deseado (rectificado, corregido, georeferenciado, según para que sirvan las coordenadas) el programa busca los valores de esta posición en los rásters de referencia (uno por el eje de las X y el otro por el eje de las Y), lo que le acaba proporcionando el píxel concreto en la imagen a corregir que está más cercano a las coordenadas de los rásters de referencia. El valor en el ráster origen se asignará a este píxel del ráster de salida cuando el método de remuestreo sea el vecino más cercano, o se interpolará a partir de los vecinos en los otros métodos de remuestreo disponibles. Por defecto, el archivo de salida tendrá la misma envolvente, lado de píxel y sistema de referencia que los rásters de referencia XY.
Nota sobre el formato de los ficheros COR:
Los ficheros COR contienen los puntos de control y, opcionalmente, de test, tienen el formato siguiente:
Nombre_de_punts [Coments]
X_SistOri1 Y_SistOri1 X_SistDest1 Y_SistDest1 [Z_SistDest1] [Coments1]
: : : : : :
- La coordenada Z_SistDest1 no es necesaria en las dos primeras opciones del programa.
- Los puntos de test (optativos) se situarán, con el mismo formato, debajo de esta secuencia. Es necesario indicar, al principio del bloque correspondiente, cuántos hay.
- El fichero puede terminar con comentarios de extensión indefinida, que el programa no conserva y que son substituidos por los resultados del ajuste.
- Las coordenadas del "Sistema Origen" deben ser cartesianas, es decir, deben crecer hacia la derecha en x y hacia arriba en y. La coordenada 0,0 puede situarse en cualquier punto del fichero origen o incluso fuera del mismo.
Este formato puede generarse con un editor de texto o, más fácilmente, partiendo de un fichero de puntos digitalizados sobre la imagen o vector original a corregir utilizando el programa VECCOR.
Para imágenes ráster y en las opciones del programa que no requieren la introducción de la resolución ni el envolvente del fichero de salida, éste hereda estos parámetros del MDE. Los valores máximos de la envolvente del fichero de salida se adaptan en función del valor de la resolución de salida (res), usando la expresión siguiente:
Xmáxima = Xmínima + res * redondear_por_exceso((Xmáxima-Xmínima)/res)
Ymáxima = Ymínima + res * redondear_por_exceso((Ymáxima-Ymínima)/res)
El número de columnas y filas de la imagen final pueden deducirse de:
Ncolumnas = (Xmáxima-Xmínima)/res
Nfilas = (Ymáxima-Ymínima)/res
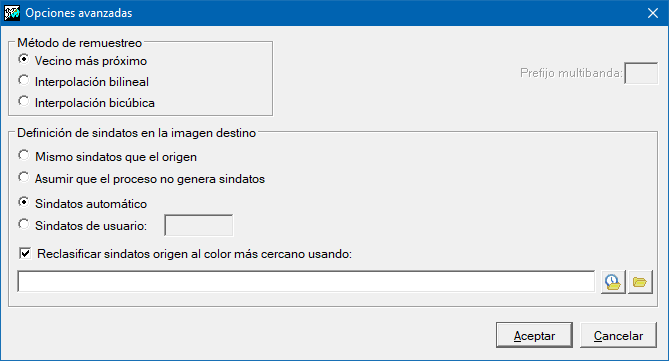
El valor de fondo o sindatos es el valor que se escribirá en el fichero corregido cuando el fichero a corregir no tenga datos para las celdas de salida en aquella posición. El usuario puede decidir el valor de sindatos o puede permitir al programa tomar la decisión. En este caso, por defecto, será igual al de entrada si existiera o, si en origen no hay, 255 para imágenes byte/byte-RLE o el valor negativo más pequeño posible para los demás formatos. Si la imagen a corregir era byte/byte-RLE y no tenía sindatos definido, y al corregir se generan valores sindatos, por defecto los valores originales válidos que en destino corresponden a sindatos se saturarán. En imágenes de 24-bits reducidas a 8-bits con paleta optimizada este hecho puede provocar una visualización incorrecta y por tanto se da la opción de que el programa reclasifique estos valores al índice de color más cercano, de manera que la visualización queda prácticamente inalterada.
El programa soporta modelos digitales de elevaciones de tipo de datos byte, integer (short) y real, comprimidos o no-comprimidos.

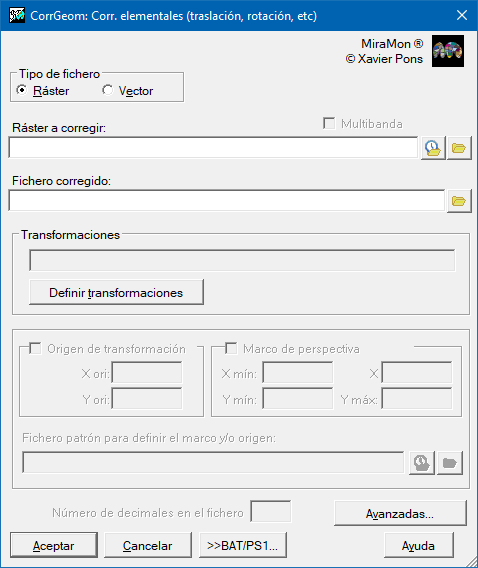
Caja de diálogo de la aplicación
 |
 |
 |
 |
 |
 |
 |
| Caja de diálogo de CorrGeom |

Ejemplos gráficos
Correcciones polinómicas de primer grado
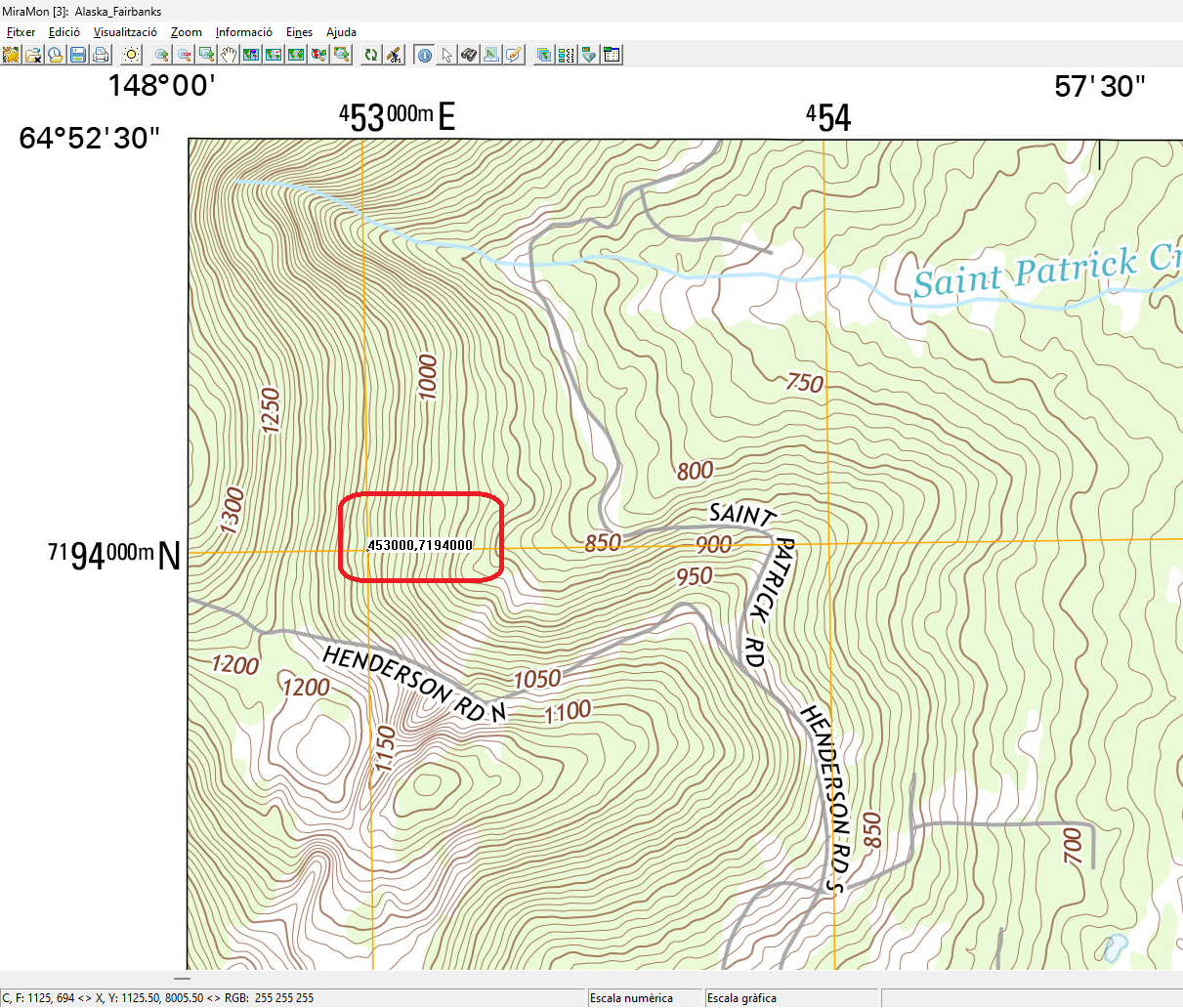 |
Detalle de la colocación de un punto de control en la coordenada UTM-06N (453000,7194000),
datum Norteamérica 1983, en un mapa topográfico 1:25000 del USGS en Alaska Fairbanks.
La colocación esmerada de un punto en cada uno de los 4 extremos del mapa permite obtener, georeferenciado,
el documento cartográfico con un RMS que presenta un ajuste de 28 cm con el documento escaneado
(en realidad, puesto que el mapa es a escala 1:25000 el RMS real sobre el terreno debe ser de unos 5 m). |
Correcciones polinómicas con Z
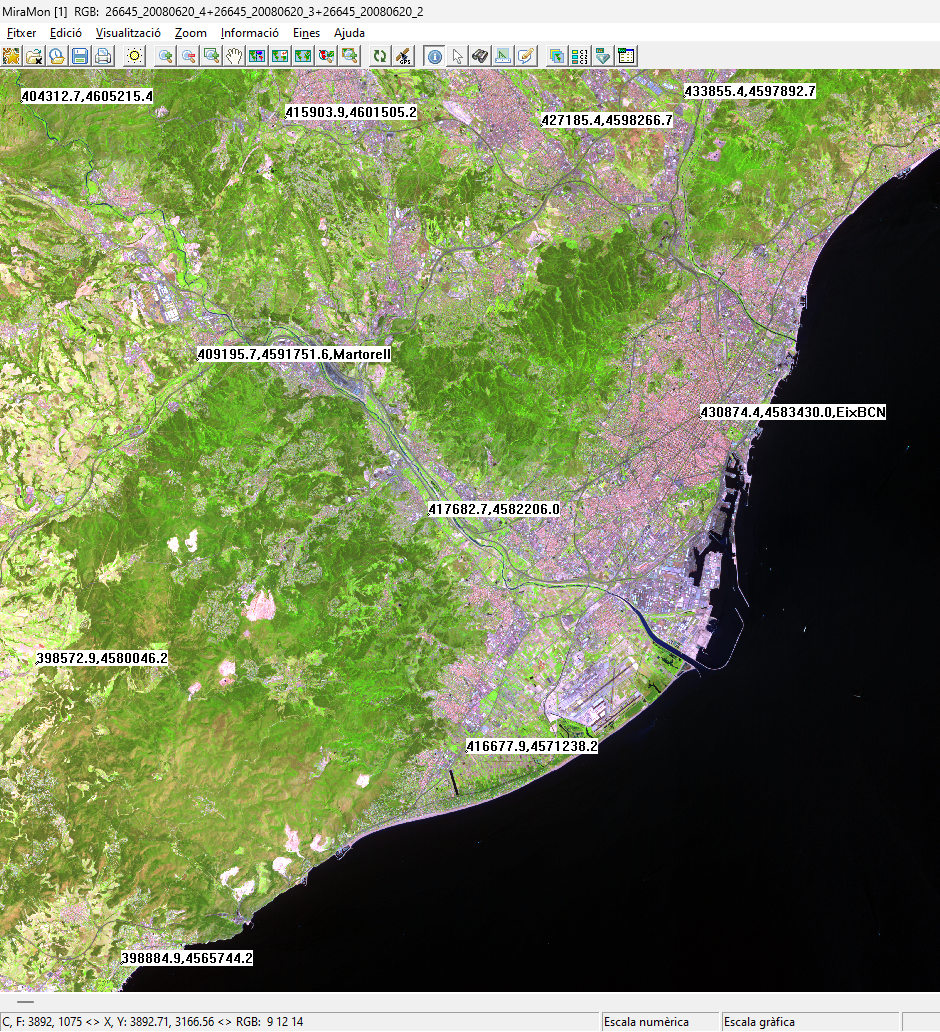 |
 |
| Puntos de ajuste ubicados en una imagen SPOT ((c) SPOT-Image) |
Aspecto general de la corrección de la anterior imagen SPOT sobre
una ortofoto del ICGC (las zonas con sindatos se muestran transparentes). |
 |
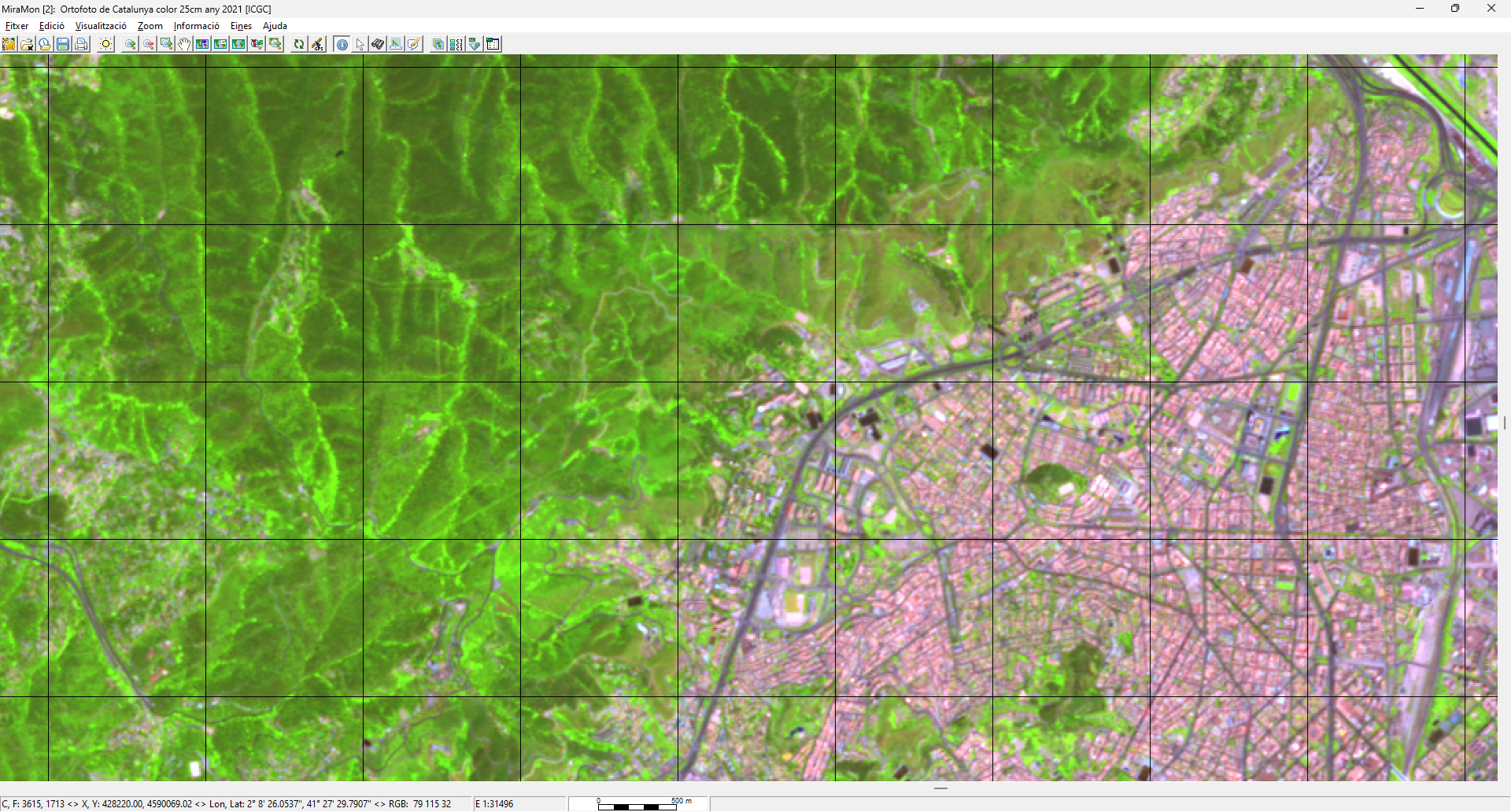 |
| Detalle de la corrección de la anterior imagen SPOT comparada con una imagen del ICGC. La red de referencia tiene un lado de 1 km. |
Correcciones con ecuaciones de colinealidad
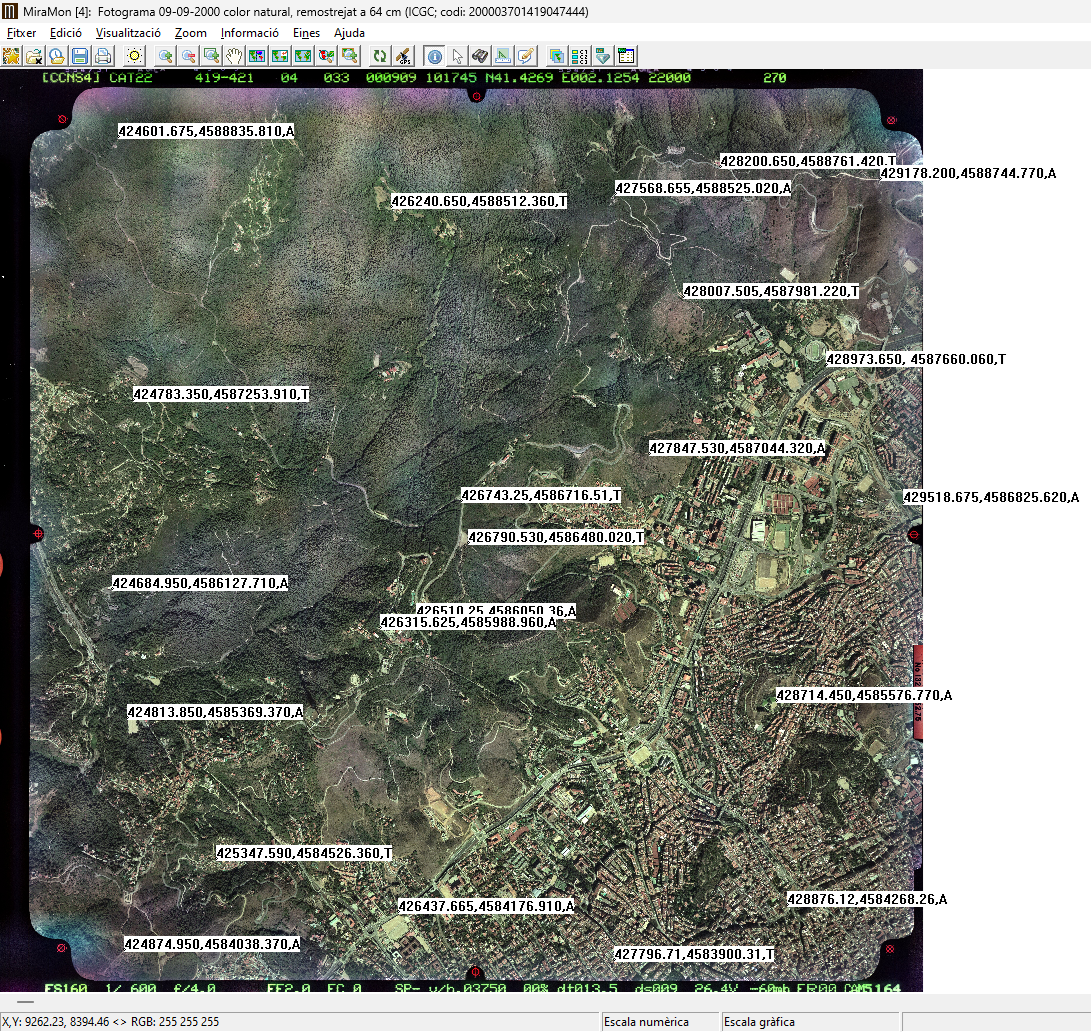 |
 |
| Puntos de ajuste (A) y prueba (T) situados en un marco del Instituto Cartográfico y Geológico de Cataluña (ICGC). |
Detalle de la corrección del anterior fotograma, convertido en una ortofoto (izquierda) comparado con una ortofoto del ICGC (derecha) para apreciar el muy buen ensamblaje geométrico conseguido. Cada píxel de la imagen corresponde a 50 cm. |
Ejemplos de sintaxis
Para imágenes ráster
CorrGeom 1 MAP MA2 LANDSAT.img LND 0 450000 480500 4724500 4750000 30 /NODATA=0
CorrGeom 2 MAP NUL LANDSAT.img LND 1 X X X X 30
CorrGeom 4 MAP MA2 LANDSAT.img ORTOLND 1 MDE30
CorrGeom 6 MAP MA2 FOTOSCAN.img ORTOFOT 1 MDE05 400 20 153 1475 1512
Para ficheros vectoriales
CorrGeom 1 MUNIPC_1 MUNIPC_2 MUNI_1.pnt MUNI_COR
CorrGeom 2 MUNIPC_1 NUL MUNI_1.arc MUNI_COR
CorrGeom 1 MUNIPC_1 MUNIPC_2 MUNI_1.vec MUNI_COR 0
Para transformaciones geométricas (afines y en perspectiva)
Traslación de 6.5 unidades en dirección vertical positiva:
CorrGeom 7 LANDSAT.img LND 0 T 0 6.5
Traslación de 7 unidades en dirección horizontal negativa:
CorrGeom 7 LANDSAT.img LND 0 T -7 0
Rotación de 45 grados en el sentido horario:
CorrGeom 7 LANDSAT.img LND 0 R 45
Rotación de 45 grados en el sentido antihorario:
CorrGeom 7 LANDSAT.img LND 0 R -45
Escalado de razón 2 (en las dos direcciones: vertical y horizontal) más rotación horaria de 90 grados:
CorrGeom 7 LANDSAT.img LND 0 E 2 2 R 90
Ligera inclinación en la dirección horizontal hacia la derecha:
CorrGeom 7 LANDSAT.img LND 0 I x 0.1
Inclinación del 50% en la dirección hortizontal hacia la izquierda:
CorrGeom 7 LANDSAT.img LND 0 I x -1
Perspectiva de unos puntos situados sobre un ráster del que también hemos hecho perspectiva (de 0.5). Supongamos que el ráster tiene como envolvente (XMIN, YMIN)=(0,10), (XMAX, YMAX)=(4500, 6000)
CorrGeom 7 MUNI_1.pnt MUNI_COR P 0.5 /XMIN=0 /XMAX=4500 /YMIN=10 /YMAX=6000
Observamos que si no aplicáramos estos parámetros optativos, los puntos no se adaptarían al ráster modificado.
Rotación de unos puntos situados sobre un ráster del que también hemos realizado rotación (de 45 grados). Supongamos que el ráster tiene como envolvente (XMIN, YMIN)=(0,10), (XMAX, YMAX)=(4500, 6000)
CorrGeom 7 MUNI_1.pnt MUNI_COR R 45 /XORI=0 /YORI=10
Observamos que si no aplicáramos estos parámetros optativos, los puntos no se adaptarían al ráster modificado.
Escalado de cm a m y después trasladar 4000000 m a las Y's.
Los argumentos de las transformaciones afines son transformados por el propio programa, por tanto, hay que pensarlo como:
Escalaje de cm a m. Trasladar 400000000 cms a las Y.
CorrGeom 7 Fitxer.arc Fitxer_sor.arc E 100 100 T 0 400000000
Para ajuste basado en puntos de referencia
CorrGeom 8 Fitx_in.img Fitx_out.img Fitx_X.img Fitx_Y.img 0 x x x x
CorrGeom 8 Fitx_multi_in.img Directori Fitx_X.img Fitx_Y.img 0 x x x x /MULTIBANDA /PREFIX=apr_

Sintaxis
Sintaxis:
- CorrGeom 1 FichCor FichCorErr FichRasOri FichRasSal Remuestreo xMin xMax yMin yMax res [/NODATA] [/PALETA] [/MULTIBANDA] [/PREFIX] [/SIST_DEST]
- CorrGeom 1 FichCor FichCorErr FichVecOri FichVecSal [/N_DECIMALS] [/SIST_DEST]
- CorrGeom 2 FichCor FichCorErr FichRasOri FichRasSal Remuestreo xMin xMax yMin yMax res [/NODATA] [/PALETA] [/MULTIBANDA] [/PREFIX] [/SIST_DEST]
- CorrGeom 2 FichCor FichCorErr FichVecOri FichVecSal [/N_DECIMALS] [/SIST_DEST]
- CorrGeom 3 FichCor FichCorErr FichRasOri FichRasSal Remuestreo MDE [/NODATA] [/PALETA] [/MULTIBANDA] [/PREFIX] [/MDE_MULTIBANDA]
- CorrGeom 4 FichCor FichCorErr FichRasOri FichRasSal Remuestreo MDE [/NODATA] [/PALETA] [/MULTIBANDA] [/PREFIX] [/MDE_MULTIBANDA]
- CorrGeom 5 FichCor FichCorErr FichRasOri FichRasSal Remuestreo MDE [/NODATA] [/PALETA] [/MULTIBANDA] [/PREFIX] [/MDE_MULTIBANDA]
- CorrGeom 6 FichCor FichCorErr FichRasOri FichRasSal Remuestreo MDE Resolución Iteraciones OpcPosición OpcActitud OpcFocal OpcPtoPrinc [/XCAM] [/YCAM] [/ZCAM] [/WCAM] [/FCAM] [/KCAM] [/FOCAL] [/ANALOG] [/DIGITAL] [/XPP] [/YPP] [/PMPCONTROL] [/PMRASTER] [/NODATA] [/PALETA] [/MULTIBANDA] [/PREFIX] [/MDE_MULTIBANDA]
- CorrGeom 7 FichRasOri FichRasSal Remuestreo [T] [Tx] [Ty] [E] [Ex] [Ey] [I] [Id] [Ir] [R] [g] [P] [Pr] [M] [Md] [/NODATA] [/PALETA] [/MULTIBANDA] [/PREFIX] [/MDE_MULTIBANDA] [/YORI] [/XMAX] [/XORI] [/YMIN] [/XMIN] [/YMAX]
- CorrGeom 7 FichVecOri FichVecSal [T] [Tx] [Ty] [E] [Ex] [Ey] [I] [Id] [Ir] [R] [g] [P] [Pr] [M] [Md] [/YMIN] [/XMIN] [/YMAX] [/YORI] [/XMAX] [/XORI] [/N_DECIMALS]
- CorrGeom 8 FichRasOri FichRasSal FichCoorX FichCoorY Remuestreo RetXMin RetXMax RetYMin RetYMax [/MULTIBANDA] [/PREFIX] [/NODATA] [/PALETA] [/SIST_DEST]
Opciones:
- 1:
Ajuste polinómico de primer grado (caso ráster).
- 1:
Ajuste polinómico de primer grado (caso vector).
- 2:
Ajuste polinómico de segundo grado (caso ráster).
- 2:
Ajuste polinómico de segundo grado (caso vector).
- 3:
Ajuste con polinomio con Z para las columnas y polinomio de 1r grado sin Z para las filas.
- 4:
Como opción 3 pero con cabeceo constante y Z para las filas.
- 5:
Como opción 3 pero con cabeceo variable y Z para las filas.
- 6:
Ecuaciones de colinealidad.
- 7:
Transformaciones geométricas (afines y perspectiva) (caso ráster).
- 7:
Transformaciones geométricas (afines y perspectiva) (caso vector).
- 8:
Ajuste basado en puntos de referencia.
Parámetros:
- FichCor
(Control -
Parámetro de entrada): Es el fichero que contiene los puntos de control en formato COR.
- FichCorErr
(Control error -
Parámetro de salida): Es el nombre del fichero COR que contendrá las ecuaciones y los errores del ajuste y el test. Puede indicar NUL para correcciones automáticas donde no desee generar este fichero.
- FichRasOri
(Fichero Imagen -
Parámetro de entrada): Es el fichero ráster a corregir (con extensión).
- FichRasSal
(Fichero raster de salida -
Parámetro de salida): Es el nombre del fichero corregido (sin extensión) o el nombre del directorio de los ficheros corregidos para el caso multibanda.
- Remuestreo
(Tipo remuestreo -
Parámetro de entrada): Criterio para decidir el valor del píxel de salida (tipo de remuestreo):
- 0: Vecino más cercano (mapas temáticos; preservar radiometría original).
- 1: Interpolación bilineal (imágenes para fotointerpretación; MDE).
- 2: Interpolación bicúbica (como 1; resultados suavizados pero más lento).
- xMin
(X Mínima -
Parámetro de entrada): Es la coordenada X mínima. Indique 'x x x x' si quiere que el programa las calcule (se corregirá todo el ráster origen).
- xMax
(X Máxima -
Parámetro de entrada): Es la coordenada X máxima. Indique 'x x x x' si quiere que el programa las calcule (se corregirá todo el ráster origen).
- yMin
(Y mínima -
Parámetro de entrada): Es la coordenada Y mínima. Indique 'x x x x' si quiere que el programa las calcule (se corregirá todo el ráster origen).
- yMax
(Y màxima -
Parámetro de entrada): Es la coordenada Y màxima. Indique 'x x x x' si quiere que el programa las calcule (se corregirá todo el ráster origen).
- res
(Resolución de salida -
Parámetro de entrada): Resolución de la imagen de salida en unidades mapa.
- FichVecOri
(Fichero vectorial a corregir -
Parámetro de entrada): Es el fichero vectorial a corregir (con extensión).
- FichVecSal
(Fichero vectorial de salida -
Parámetro de salida): Es el nombre del fichero corregido (sin extensión).
- MDE
(Modelo Digital de Elevaciones -
Parámetro de entrada): Fichero ráster con el modelo digital de elevaciones de la zona.
- Resolución
(Resolución -
Parámetro de entrada): Es la resolución en ppp (píxels por pulgada o dpi) para imágenes escaneadas o fotografías digitales.
- Iteraciones
(Iteraciones -
Parámetro de entrada): Número máximo de iteraciones en el cálculo del ajuste de los parámetros de colinealidad (sugerimos 20).
- OpcPosición
(Opciones de posición -
Parámetro de entrada): Opción (de posición) que define si los parámetros implicados en las ecuaciones de colinealidad son fijos y conocidos (3), son estimados (2) o son desconocidos (0). El valor (1) es para el caso especial de la posición cuando solamente se tiene una estima de la altitud de vuelo, pero no de la posición X,Y del avión.
- OpcActitud
(Opciones de actitud -
Parámetro de entrada): Opción (de actitud) que define si los parámetros implicados en las ecuaciones de colinealidad son fijos y conocidos (3), son estimados (2) o son desconocidos (0).
- OpcFocal
(Opciones focal -
Parámetro de entrada): Opción (de focal) que definen si los parámetros implicados en las ecuaciones de colinealidad son fijos y conocidos (3), son estimados (2) o son desconocidos (0).
- OpcPtoPrinc
(Opciones punto principal -
Parámetro de entrada): Opción (punto principal) que definen si los parámetros implicados en las ecuaciones de colinealidad son fijos y conocidos (3), son estimados (2) o son desconocidos (0).
- T
(Translación -
Parámetro de entrada): Indica que la transformación geométrica a efectuar es una translación.
- Tx
(Valor X -
Parámetro de entrada): Valor en las unidades del fichero de origen para la componente horizontal de la translación.
- Ty
(Valor Y -
Parámetro de entrada): Valor en las unidades del fichero de origen para la componente vertical de la translación.
- E
(Escalado -
Parámetro de entrada): Indica que la transformación geométrica a efectuar es un escalado.
- Ex
(Valor X -
Parámetro de entrada): Razón de escalado horizontal.
- Ey
(Valor Y -
Parámetro de entrada): Razón de escalado vertical. Ex y Ey no pueden valer 0 o 1 simultáneamente. Ni Ex ni Ey pueden valer 0 porque no se permite colapsar el resultado en un punto y por tanto el programa no acepta estos valores.
- I
(Inclinación -
Parámetro de entrada): Indica que la transformación geométrica a efectuar es una inclinación.
- Id
(Eje inclinación -
Parámetro de entrada): Si se desea inclinar en dirección horizontal el parámetro debe valer "x". Si se desea inclinar en dirección vertical el parámetro debe valer "y".
- Ir
(Razón inclinación -
Parámetro de entrada): Indica la razón de inclinación. El valor 0 indica que no hay inclinación y como mayor sea la razón, mayor inclinación. También acepta un número negativo. Valores positivos indican inclinación hacia la derecha (en sentido horizontal) o hacia arriba (en sentido vertical) y valores negativos indican inclinación hacia la izquierda (en sentido horizontal) o hacia abajo (en sentido vertical).
- R
(Rotación -
Parámetro de entrada): Indica que la transformación geométrica a efectuar es una rotación.
- g
(grados -
Parámetro de entrada): Indica los grados de rotación en el sentido horario. Si se desea en sentido inverso al horario debe anteponerse el signo "menos" ("-"). El rango de valores permitidos es de -360 a 360.
- P
(Perspectiva -
Parámetro de entrada): Indica que la transformación geométrica a efectuar es una perspectiva.
- Pr
(Razón perspectiva -
Parámetro de entrada): Indica la razón de perspectiva. El valor que adopta debe ser un real mayor o igual que cero y menor estricto que 1. Si el valor es 0, el resultado no se modifica y como más cercano a 1 sea, más se deforma tendiendo a un punto de fuga infinito.
- M
(Reflejo -
Parámetro de entrada): Indica que la transformación geométrica a efectuar es un reflejo.
- Md
(Dirección reflejo -
Parámetro de entrada): Indica la dirección del reflejo. Si se desea un reflejo respecto al eje horizontal debe usarse el valor 'x' (o 'X'). Si se desea un reflejo respecto al eje vertical debe usarse el valor 'y' (o 'Y').
- FichCoorX
(Fichero coordenadas X -
Parámetro de entrada): Es el nombre del fichero ráster (con extensión) con coordenadas X donde se busca el valor en el fichero origen.
- FichCoorY
(Fichero coordenadas Y -
Parámetro de entrada): Es el nombre del fichero ráster (con extensión) con coordenadas Y donde se busca el valor en el fichero origen.
- RetXMin
(X mínima a recortar -
Parámetro de entrada): Se indica la coordenada X mínima del ámbito del fichero destino. Si se indica 'x', se escogerá la X mínima del archivo de coordenadas X e Y.
- RetXMax
(X máxima a recortar -
Parámetro de entrada): Se indica la coordenada X máxima del ámbito del fichero destino. Si se indica 'x', se escogerá la X mínima del archivo de coordenadas X e Y.
- RetYMin
(Y mínima a recortar -
Parámetro de entrada): Se indica la coordenada Y mínima del ámbito del fichero destino. Si se indica 'x', se escogerá la X mínima del archivo de coordenadas X e Y.
- RetYMax
(Y máxima a recortar -
Parámetro de entrada): Se indica la coordenada Y máxima del ámbito del fichero destino. Si se indica 'x', se escogerá la X mínima del archivo de coordenadas X e Y.
Modificadores:
/XCAM=
(X cámara)
Coordenada X de la cámara o sensor en el sistema de referencia destino, tanto si son posiciones ya conocidas, como valores estimados. Si sólo se indica /ZCAM, se hace referencia a un valor estimado de la altitud de vuelo. (Parámetro de entrada) /YCAM=
(Y cámara)
Coordenada Y de la cámara o sensor en el sistema de referencia destino, tanto si son posiciones ya conocidas, como valores estimados. Si sólo se indica /ZCAM, se hace referencia a un valor estimado de la altitud de vuelo. (Parámetro de entrada) /ZCAM=
(Z cámara)
Coordenada Z de la cámara o sensor en el sistema de referencia destino, tanto si son posiciones ya conocidas, como valores estimados. Si sólo se indica /ZCAM, se hace referencia a un valor estimado de la altitud de vuelo. (Parámetro de entrada) /WCAM=
(Omega)
Indica, en grados, el ángulo de actitud "omega" del sensor, sea éste fijado o estimado. (Parámetro de entrada) /FCAM=
(Fi)
Indica, en grados, el ángulo de actitud "fi" del sensor, sea éste fijado o estimado. (Parámetro de entrada) /KCAM=
(Kappa)
Indica, en grados, el ángulo de actitud "kappa" del sensor sea éste fijado o estimado. (Parámetro de entrada) /FOCAL=
(Focal)
Distancia focal en mm (Parámetro de entrada) /ANALOG
(Cámara analógica)
Si la focal de la cámara es desconocida, conocer si es digital o analógica (este caso) ayuda a tomar un valor inicial que converja más rápidamente al valor ajustado. (Parámetro de entrada) /DIGITAL
(Cámara digital)
Si la focal de la cámara es desconocida, conocer si es digital o analógica ayuda a tomar un valor inicial que converja más rápidamente al valor ajustado. (Parámetro de entrada) /XPP=
(XPP)
Coordenada X conocidas o iniciales del punto principal en el sistema de referencia origen. (Parámetro de entrada) /YPP=
(YPP)
Coordenada Y conocidas o iniciales del punto principal en el sistema de referencia origen. (Parámetro de entrada) /PMPCONTROL=
(Punto medio punts de control)
Si la localización del punto principal es desconocida, puede indicarse si los valores iniciales se calcularán a partir de la media de los puntos de control o del punto medio del envolvente del ráster a corregir. (Parámetro de entrada) /PMRASTER=
(Punt medio raster)
Punt medio raster (Parámetro de entrada) /MDE_MULTIBANDA (Model Digital Elevaciones MULTIBANDA) Para corregir a la vez rásters multibanda que tienen diferentes lados de píxel con un MDE que tiene una banda para cada valor no repetido de lado de píxel. (Parámetro de entrada) /YMIN= (Y mínima de la zona a aplicar transformación.) Coordenada Y mínima del ámbito en el que se desea aplicar la transformación. Sólo es útil cuando se realiza una perspectiva ya que en las transformaciones sin perspectiva se usa /XORI, /YORI. (Parámetro de entrada) /XMIN= (X mínima de la zona a aplicar transformación.) Coordenada X mínima del ámbito en el que se desea aplicar la transformación. Sólo es útil cuando se realiza una perspectiva ya que en las transformaciones sin perspectiva se usa /XORI, /YORI. (Parámetro de entrada) /YMAX= (Y màxima de la zona a aplicar transformación.) Coordenada Y máxima del ámbito en el que se desea aplicar la transformación. Sólo es útil cuando se realiza una perspectiva ya que en las transformaciones sin perspectiva se usa /XORI, /YORI. (Parámetro de entrada) /YORI= (Origen transformación en el eje Y) Indica el origen en el eje Y de la transformación en caso de que haya alguna. (Parámetro de entrada) /XMAX= (X màxima de la zona a aplicar transformación.) Coordenada X máxima del ámbito en el que se desea aplicar la transformación. Sólo es útil cuando se realiza una perspectiva ya que en las transformaciones sin perspectiva se usa /XORI, /YORI. (Parámetro de entrada) /XORI= (Origen transformación en el eje X) Indica el origen en el eje X de la transformación en caso de que haya alguna. (Parámetro de entrada) /N_DECIMALS= (Número de decimales) Número de cifras decimales en las coordenadas del vector de salida. Solo se aplica para ficheros VEC. (Parámetro de entrada) /MULTIBANDA (MULTIBANDA) Para corregir a la vez rásters multibanda y generar como resultado un ráster multibanda con las correspondientes bandas corregidas. (Parámetro de entrada) /PREFIX= (Prefijo) Prefijo que se añade a los nombres de los ficheros originales para determinar los nombres de los ficheros corregidos para el caso multibanda. Por defecto este prefijo es c_. (Parámetro de entrada) /NODATA= (sindatos) Valor del sindatos para la imagen corregida. Si el usuario sabe que con toda seguridad (evaluando la geometría de la transformación, el ámbito y rango del MDE...) que no habrá NODATA puede usarse el valor "NONE". (Parámetro de entrada) /PALETA= (Paleta) Paleta (p25, pal, p65) o tabla de simbolización (dbf) que determinará qué índice de color es el color más cercano al índice de sindatos para la imagen corregida. (Parámetro de entrada) /SIST_DEST= (Sistema de referencia de destino) Identificador del sistema de proyección del fichero de salida. (Parámetro de entrada)














