| Presentación y opciones | Cajas de diálogo de la aplicación |
| Ejemplos gráficos | Sintaxis |
Como en el caso de otros procedimientos de cálculo, la interpolación a partir de puntos puede dar resultados notablemente diferentes según las opciones de la aplicación escogidas. El método escogido, la distancia umbral, la ponderación a aplicar, la utilización de máscaras de exclusión, etc, pueden ayudar enormemente a mejorar los resultados. El conocimiento de los datos con que se trabaja y la realización de pruebas tentativas variando diferentes parámetros son a menudo de gran ayuda para tomar decisiones sobre cómo usar estos parámetros. Además, si se puede, conviene reservar un conjunto de puntos independientes aleatoriamente distribuidos para poder realizar una evaluación cuantitativa de los resultados (test).
En los cálculos de cuantiles, como la mediana, puede indicarse, con el modificador /MEDIANA_EMPAT=, el tipo de desempate a usar para su cálculo cuando la posición del cuantil sea entre dos valores de la serie. Para más información se puede consultar sintaxis general.
En la actual versión existen cinco posibles métodos de interpolación: inverso de la distancia, función spline, superficies de tendencia, kriging y estadísticas de vecindad.
Por el método del inverso de la distancia, la interpolación del punto problema (celda) se realiza asignando pesos a los valores de los puntos de muestreo en función inversa de la distancia que separa el centro de píxel del punto problema. Esta distancia puede calcularse de manera euclidiana, o utilizando un cálculo simplificado (distancia de Manhattan). Se puede consultar más detalles en https://en.wikipedia.org/wiki/Inverse_distance_weighting.
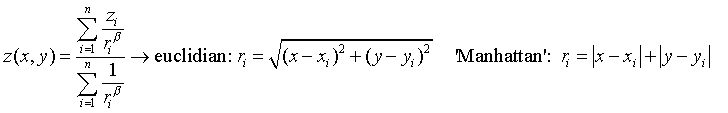
Por el método spline se determina la función regular, continua y derivable, o el conjunto de funciones si dividimos el ámbito global en diferentes regiones, que se adapte mejor a los puntos de muestreo sin perder sus propiedades de continuidad. Para conocer más detalles de la expresión analítica de esta función puede consultar:
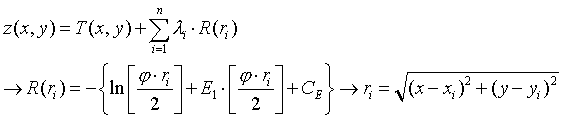
Por el método de generación de superficies de tendencia, se trata de ajustar una función polinómica respecto de las coordenadas X, Y de grado 1, 2 o 3 que dará lugar a una superficie suave, continua y derivable resultado del ajuste. Este ajuste se realiza por mínimos cuadrados y permitirá determinar los coeficientes de cada término del polinomio.
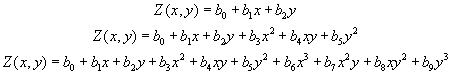
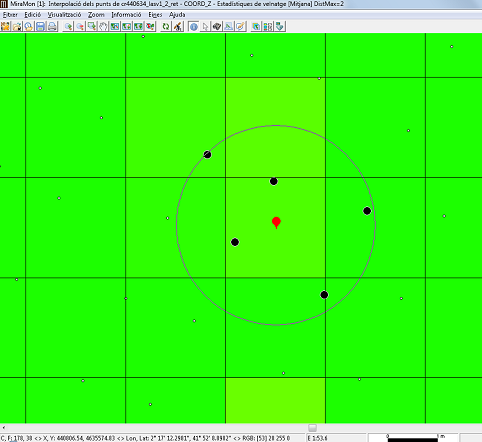
Con el método de estadísticas de vecindad, se asigna a cada celda el estadístico designado (media, mediana, máximo, mínimo, rango, desviación estándar, media de las desviaciones absolutas respecto de la mediana o número de ocurrencias, percentil), calculado considerando todos los puntos que se encuentran dentro de un círculo definido por un radio, o dentro de un cuadrado definido por un lado, ubicados en el centro de cada celda que se quiere interpolar. A diferencia de otros métodos de InterPNT, y en particular del método que hace la interpolación por ponderación del inverso de la distancia elevada a un exponente determinado por el usuario pero que también limita este cálculo a un cierto radio de distancia (distancia máxima), en el modo de estadísticas de vecindad una vez se seleccionan todos los puntos presentes dentro del ámbito (circular o cuadrado) indicado, no se efectúa ninguna ponderación sino que directamente se hace el cálculo pedido, que puede ser una medida de centralidad de los diferentes valores (media o mediana), de dispersión de estos valores (máximo, mínimo, rango, desviación estándar, media de las desviaciones absolutas respecto de la mediana) o, simplemente, un recuento del número de valores disponibles (número de ocurrencias).
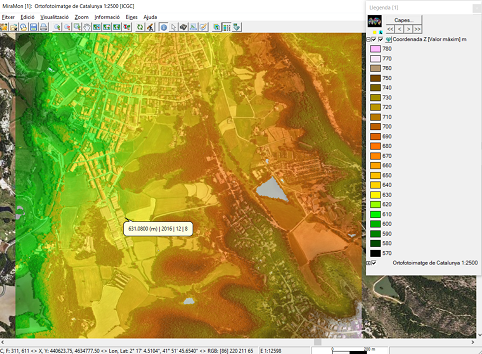
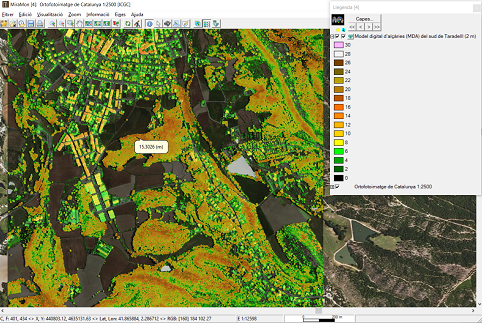
Este es un método típico para el procesamiento de datos lidar, y particularmente para la producción de Modelos Digitales de Superficies (MDS) o de Modelos Digitales de Alturas (MDA). En estas dos aplicaciones se suele tomar la cota más alta obtenida por el lidar en el ámbito de la celda del ráster a obtener. Este ámbito puede ser el área de la celda si la densidad de puntos es lo suficientemente alta en relación al tamaño de la celda, o algo mayor (por ejemplo un radio 1.5 veces el lado de la celda); se pueden consultar las opciones específicas, más abajo, para más detalles.
Si la densidad de puntos es muy alta se puede pedir, en vez del máximo, un percentil 90, etc, con lo que se reduce la probabilidad de adoptar como superficie real algún artefacto del sensor como la detección de pájaros volando en ese momento. Con otras estadísticas, como las de dispersión, se pueden obtener interesantes datos de la estructura vertical de las masas de vegetación. Finalmente, con la elección de estadísticas de mínimo, combinadas con la selección de puntos que correspondan a retornos únicos (información disponible en uno de los campos de la tabla de atributos) y de intensidades de retorno elevadas (dato también disponible en otro campo), y con radios de exploración muy grandes (varias veces el lado de celda a obtener), se puede obtener un Modelo Digital de Elevaciones. Si ya se dispone de un MDE, o éste se ha calculado con los datos lidar como se acaba de describir, se puede obtener un MDA (los datos altimétricos de la vegetación o de las construcciones humanas se miden desde el suelo y no desde el nivel del mar); en este caso lo más práctico es, antes de ejecutar InterPNT, ejecutar la aplicación CombiCap en la forma MDE+PNT-->PNT y con el modo de transferencia de campos estadísticos utilizando la interpolación bilineal, donde el segundo PNT obtendrá las elevaciones a cada punto; a continuación se genera un campo vacío de tipo numérico y típicamente con 2 o 3 decimales para que, con el uso de CalcImg, sea llenado con la altura del punto (calculada haciendo el resto entre la altitud obtenida por el lidar y la elevación resultante de CombiCap). Esta altura es la que se somete a InterPNT para obtener el MDA.
Operación general
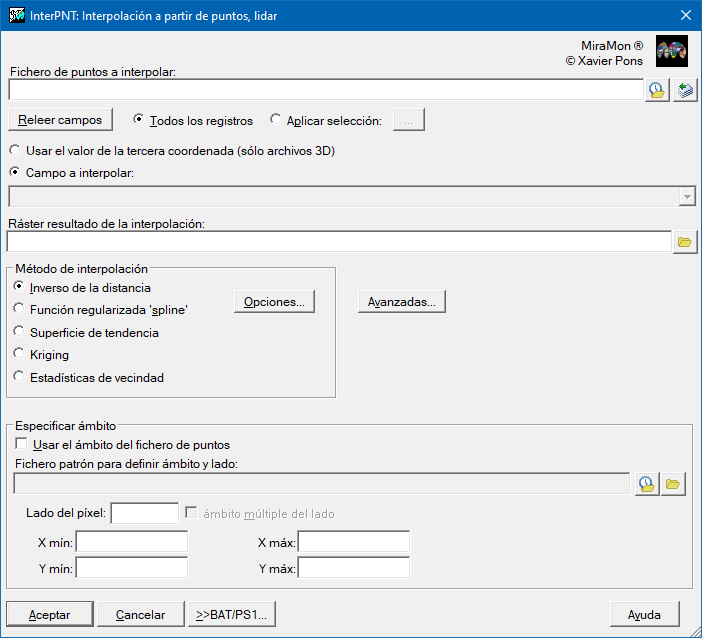
En primer lugar, hay que escoger si se quiere usar el valor de la tercera coordenada (en el caso de archivos 3D) o seleccionar un campo a interpolar de la base de datos asociada al fichero de puntos. En el caso de escoger un campo de la base de datos, hay que seleccionar un campo numérico. Aunque los valores de este campo puedan ser enteros, el interpolador tratará estos datos como reales de doble precisión en todos los cálculos internos y generará un ráster resultado de reales con precisión simple.
La selección de registros es el primer filtro que escoge aquellos registros, de la base de datos del fichero de puntos, que participarán en la interpolación. La opción por defecto es 'Todos los registros', pero en muchos casos mejoraremos la calidad y la velocidad de la interpolación si excluimos aquellos registros que no deseamos que influyan en el resultado. La selección de registros se hace al construir una sentencia lógica sobre cualquier combinación de campos de la base de datos asociada al fichero de puntos. Observe que los campos implicados en la selección pueden no involucrar al campo a interpolar. Por ejemplo, si en un fichero de emisiones atmosféricas, un campo indica la comarca donde se halla cada industria y queremos interpolar cierto contaminante, podemos indicar que se interpole sólo con los valores de cierta comarca. Recomendamos utilizar la ventana que se abre a partir de la opción 'Aplicar selección' para construir esta sentencia lógica, a base de ir seleccionando los campos, operadores, valores, nexos y orden de prioridad con los botones y desplegables correspondientes. En la sección explicativa de la 'Sintaxis' de la línea de comandos detallamos los elementos de esta sentencia, que funciona de manera similar a la consulta por atributos de MiraMon.
El fichero de salida será un ráster no comprimido de valores reales (excepto cuando se definan máscaras de exclusión, entonces será comprimido y también de valores reales). Éste ráster tendrá definido el valor de fondo o sindatos en aquellas celdas en las que no haya quedado definido ningún valor posible porque aquella coordenada no verifica los criterios de las 'Opciones avanzadas', porque está dentro de una máscara de exclusión o porque no tiene un mínimo de puntos suficientes dentro de la distancia máxima de influencia.
Hay que definir la envolvente y lado de píxel de este ráster de salida, explicitando las coordenadas o ajustando la envolvente en el ámbito del fichero de puntos. Hay que hacer notar que la velocidad del proceso es muy sensible a estos valores. Un lado pequeño en una región a interpolar muy amplia sin máscara definida, dará unos valores muy precisos (suavemente variables en función de la distancia), pero el número de cálculos será muy grande y el tiempo de ejecución, largo.
Opciones para Inverso de la distancia
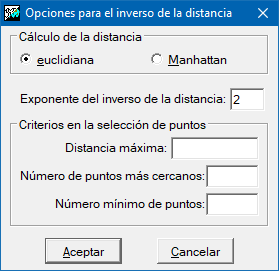
Hay que definir, en primer lugar, cómo se realizará el cálculo de la distancia; de forma euclidiana o al estilo 'Manhattan' (vea en el apartado anterior, ambas definiciones de distancia). El cálculo del valor que se asignará a cada celda es una media ponderada de los valores que toman los puntos a considerar. El peso que toma cada punto tiene una dependencia potencial respecto al inverso de la distancia entre el punto y el centro del píxel. El valor por defecto es 2, pero puede parametrizarse en la manera que el usuario juzgue más adecuada. Cuanto mayor el valor, más peso tiene el punto en su entorno inmediato, y menos peso la media de los valores circundantes.
La distancia máxima es un parámetro muy habitual que marca una región de influencia de los puntos localizados en el interior de una circunferencia, centrada en el píxel, y de radio igual a la distancia máxima indicada. Por tanto, para cada celda tendremos una distancia a partir de la cual los puntos originales no juegan ningún papel en el proceso de interpolación. Hay que tener presente que es muy razonable usar siempre este parámetro, ya que además de tener pleno sentido en la interpolación, permite reducir extraordinariamente el tiempo de ejecución.
Otro criterio interesante es definir el número máximo de puntos de los cuales dependerá el cálculo. Evidentemente siempre serán los 'n' más cercanos al centro del píxel. El reiterado proceso de ordenación que requiere la aplicación de este criterio alarga considerablemente el proceso de cálculo, pero con ello aseguramos la intervención de solamente 'n' de los más próximos. Para asegurar que el cálculo se hace con un muestreo suficiente, también podemos definir un número mínimo de puntos a participar en el cálculo de cada celda. Si no se llega a este mínimo, el valor de la celda será sindatos.
Opciones para spline
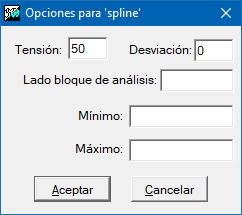
La interpolación por splines puede ser según la configuración de los puntos de muestra, bastante sensible a los parámetros de configuración. El parámetro tensión modula la suavización de la función; su valor por defecto es 40 y tensiones excesivamente bajas o elevadas pueden dar lugar a artefactos inesperados. El parámetro desviación ajusta el ruido de la muestra, el valor por defecto cero implica que la función pasa exactamente por los puntos de muestreo (interpolador exacto). El parámetro lado de bloque de análisis localiza el ajuste al dividir el ámbito en bloques de análisis en los que se restringe la solución de la función spline a esta región. Este parámetro acelera bastante los cálculos, es muy recomendable cuando disponemos de muchos puntos, pero puede llegar a producir discontinuidades no deseadas si su valor es demasiado pequeño (ventana demasiado local).
El método spline se comporta de manera óptima con muestras sin excesivas perturbaciones. Ahora bien, si localmente se tienen puntos cercanos con variaciones bruscas de la variable a interpolar, el método puede dar lugar a valores bastante alejados del rango esperado. En este caso es bastante recomendable incrementar la tensión y como opción complementaria forzar los valores de salida dentro de un máximo o un mínimo. En este caso hay que definir los modificadores /MIN_VAL y /MAX_VAL.
Si no se define el lado de análisis, la solución es única para todo el ámbito (ventana igual al ámbito), si el lado de análisis es pequeño, el ámbito se dividirá en muchas regiones independientes.
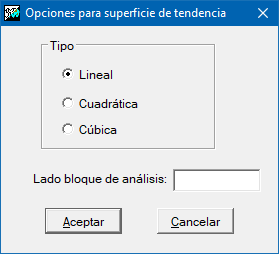
Opciones para las superficies de tendencia
El principal parámetro de esta opción es el grado que determina el orden del polinomio a ajustar. En la actual versión es posible generar superficies de primer grado o lineales, de segundo grado o cuadráticas y de tercer grado o cúbicas.
Del mismo modo que para spline, es posible generar diferentes soluciones, no estrictamente continuas, en dividir el ámbito global en subregiones más locales. Estas subregiones quedan definidas por el parámetro lado de bloque de análisis.
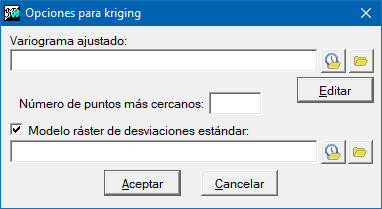
Opciones para el kriging
El método de interpolación kriging está basado en los principios de la geoestadística. Para poder aplicarlo, es necesario haber generado previamente un archivo del variograma ajustado (con extensión "vam"). Este archivo se puede generar con la aplicación Vargram, a cuya ayuda encontrará indicaciones sobre cómo modelizar el patrón espacial de la variable a analizar que da lugar al variograma que se aplicará para la interpolación con este método. En las opciones avanzadas de InterPNT, puede limitarse el número de puntos más cercanos a cada celda que participan en su valor resultante, así como obtener un ráster auxiliar de la calidad de la estimación, donde se almacenarán las desviaciones estándar para cada celda. Se puede ampliar información sobre kriging en https://en.wikipedia.org/wiki/Kriging. En castellano se ha propuesto la palabra krigeage para este método.
Opciones para las estadísticas de vecindad
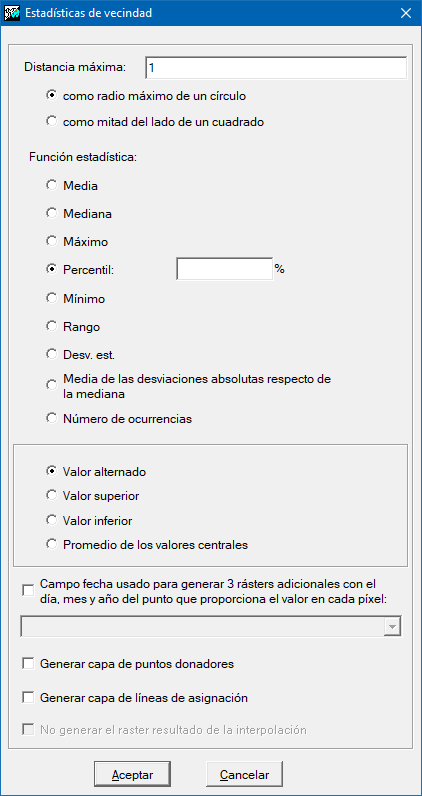
Hay que definir dos parámetros: la función estadística a utilizar, y la distancia máxima a la que un punto se considera que debe formar parte del conjunto de puntos que proporcionan los valores para el cálculo del estadístico que se transferirá a la celda del ráster de salida.
Las funciones estadísticas disponibles son la media, la mediana, el máximo, el mínimo, el rango, la desviación estándar, la media de las desviaciones absolutas respecto de la mediana y el número de ocurrencias.
Para la distancia máxima, hay dos opciones posibles: distancia máxima como radio máximo de un círculo, y distancia máxima como mitad del lado de un cuadrado. Esta última opción es típicamente utilizada cuando se desea que los puntos lidar con los que se calculará el valor del estadístico que se escribirá en la celda están ubicados estrictamente en su interior; cabe notar que, dado que el dato es la mitad del cuadrado, si se ha indicado que se quiere obtener un ráster de 2 m de lado, la distancia a indicar para la distancia máxima será 1 m. Cuando el valor del estadístico calculado proviene de un solo punto, como en el caso del mínimo y el máximo, es posible obtener capas adicionales (de nombre igual a la capa de salida y con un sufijo apropiado): Por un lado, si los datos lidar proporcionan, en respectivos campos, el día, mes y año de captura de cada punto es posible generar 3 rásters adicionales que contendrán el día, mes y año del punto que proporciona el valor en cada píxel. Por otro lado, y para propósitos didácticos y de investigación, es posible generar capas adicionales que contengan sólo los puntos donadores, o que unan con líneas los puntos donadores con el centro de la celda receptora del valor.
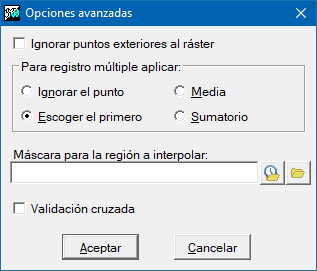
Opciones avanzadas
Las opciones avanzadas nos permiten parametrizar de la forma más ajustada posible algunos procedimientos globales de la interpolación.
En el caso en que tengamos asociado más de un registro seleccionado a un punto (p.ej. diversas mediciones en instantes diferentes de una misma fuente), podemos escoger cómo será el valor a interpolar en este punto. a) ignorar este punto con registro múltiple (por tanto, será como si no formara parte de la selección); b) escoger el valor del primer registro que verifique las condiciones de selección; c) hacer una media entre estos registros; d) hacer una suma.
Una posibilidad añadida es la elección de puntos de manera que se ignoren aquellos puntos exteriores a la envolvente definida por el ráster. Esta opción no se recomienda si los valores cercanos a los bordes del ráster de salida son importantes.
Finalmente, también podemos determinar sobre qué regiones dentro del ámbito definido, no necesitamos o no deseamos conocer el resultado de la interpolación. Utilizando un fichero que actúe como máscara de exclusión y determine cuáles zonas son útiles y cuáles no, aceleraremos considerablemente el proceso de cálculo, y obtendremos resultados más coherentes por la exclusión de zonas sin puntos; por ejemplo, si estamos interpolando elevaciones terrestres a partir de cotas, podemos excluir de la interpolación todas las zonas marítimas. Esta máscara puede ser un ráster en el que las regiones a excluir serán aquellas en que el valor de la celda es sindatos. También puede ser un vector, estructurado o no estructurado, pero siempre de tipo polígono. En este caso la zona a excluir será por defecto el polígono universal, o bien la máscara incluirá aquellos polígonos con atributo igual o diferente a un valor determinado si se define expresamente. Para vectores estructurados hay, además, que concretar qué campo de la tabla de atributos definirá la máscara.
 |
|||
 |
 |
 |
 |
 |
|||
 |
|||
| Cajas de diálogo de InterPNT | |||